题目内容
15.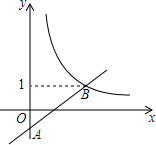 如图,在平面直角坐标系xOy中,一次函数y=ax-a(a为常数)的图象与y轴相交于点A,与函数y=$\frac{2}{x}$(x>0)的图象相交于点B(m,1).
如图,在平面直角坐标系xOy中,一次函数y=ax-a(a为常数)的图象与y轴相交于点A,与函数y=$\frac{2}{x}$(x>0)的图象相交于点B(m,1).(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请画出示意图并直接写出点P的坐标.
分析 (1)把B(m,1)代入反比例函数解析式即可求得B的坐标,进而把B的坐标代入y=ax-a根据待定系数法即可求得一次函数的解析式;
(2)根据题意画出直角三角形PAB,则PB∥x轴,根据B的坐标即可求得P的坐标.
解答 解:(1)∵函数y=$\frac{2}{x}$(x>0)的图象经过点B(m,1).
∴1=$\frac{2}{m}$,解得m=2,
∴B(2,1),
代入y=ax-a得,1=2a-a,
∴a=1,
∴一次函数的解析式为y=x-1;
(2)当∠APB=90°时,画出示意图如图,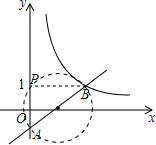
∴PB∥x轴,
∵B(2,1),
∴P(0,1).
当∠ABP=90°时,图如下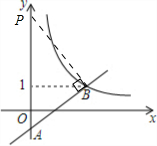
易知∠PAB=45°,故PA=2×2=4,即此时P(0,3)
综上所求的P点的坐标为(0,1)或(0,3)
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
4.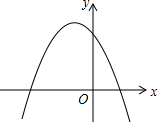 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
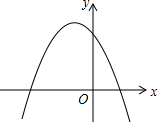 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个同号的实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
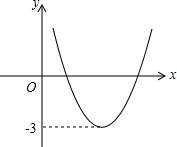 如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是有两个同号不等实数根.
如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是有两个同号不等实数根. 抛物线的部分图象如图所示,则当y<0时,x的取值范围是x>3或x<-1.
抛物线的部分图象如图所示,则当y<0时,x的取值范围是x>3或x<-1. 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC,若∠AEB=50°,求∠EBC的度数是25°.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC,若∠AEB=50°,求∠EBC的度数是25°.