题目内容
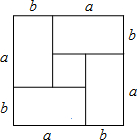 如图分割正方形,可以验证( )
如图分割正方形,可以验证( )| A、(a+b)2=a2-2ab+b2 |
| B、(a-b)2=a2-2ab+b2 |
| C、(a+b)2=(a-b)2+4ab |
| D、(a+b)(a-b)=a2-b2 |
考点:完全平方公式的几何背景
专题:
分析:观察图形可以发现中间小正方形边长为a-b,根据中间小正方形面积加4个矩形面积等于以a+b为边长的正方形的面积,即可解题.
解答:解:∵观察图形可以发现中间小正方形边长为a-b,
∴小正方形面积=(a-b)2,
∵4个矩形面积和为4ab,大的正方形面积为(a+b)2,
∴有(a+b)2=(a-b)2+4ab,
故选:C.
∴小正方形面积=(a-b)2,
∵4个矩形面积和为4ab,大的正方形面积为(a+b)2,
∴有(a+b)2=(a-b)2+4ab,
故选:C.
点评:本题考查了完全平方公式的转化,本题中分别计算小正方形面积、大正方形面积和四个矩形面积是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
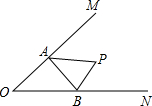 如图,已知∠MON=60°,P为∠MON内一点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数为( )度.
如图,已知∠MON=60°,P为∠MON内一点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数为( )度.| A、40 | B、60 |
| C、100 | D、120 |
 如图所示的是由小正方体搭成的几何体的俯视图.小正方形中的数字表示该位置的小正方体的个数,请画出该几何体的主视图和左视图.
如图所示的是由小正方体搭成的几何体的俯视图.小正方形中的数字表示该位置的小正方体的个数,请画出该几何体的主视图和左视图.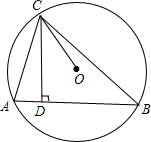 如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.
如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.