题目内容
17.列分式方程解决下列问题:一辆汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40min到达目的地.
(1)求出发后第一小时内的行驶速度;
(2)求这辆汽车到达目的地时所用的行驶时间.
分析 (1)设出发后第一小时内的行驶速度为vkm/h,根据时间=路程÷速度结合提前40min到达目的地即可得出关于v的分式方程,解之即可得出结论;
(2)根据行驶时间=路程÷速度-提前时间列式即可得出结论.
解答 解:(1)设出发后第一小时内的行驶速度为vkm/h,
根据题意得:$\frac{180}{v}$=$\frac{180-v}{1.5v}$+1+$\frac{40}{60}$,
解得:v=60,
检验:当v=60时,1.5v≠0,
∴v=60是原分式方程的解.
答:出发后第一小时内的行驶速度为60km/h.
(2)$\frac{180}{60}$-$\frac{40}{60}$=$\frac{7}{3}$(小时).
答:这辆汽车到达目的地时所用的行驶时间为$\frac{7}{3}$h.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据数量关系时间=路程÷速度列出关于v的分式方程;(2)根据数量关系行驶时间=路程÷速度-提前时间列式计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知A(-1,y1)、B(2,y2)、C(-3,y3)在函数y=-2(x+1)2+3的图象上,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
6.已知代数式4x-12+8y的值是8,则代数式x+2y的值是( )
| A. | 5 | B. | 20 | C. | -1 | D. | 2 |

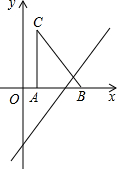 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).