题目内容
 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径, |
| AB |
 |
| AF |
考点:圆周角定理,相似三角形的判定与性质
专题:
分析:由A,F把半圆三等分,得到∠ACB=∠CBF=30°,而BC=12,得到AB=6,再根据∠BAD=∠ACB,得到∠BAD=30°,所以BD=3,AD=3
,在Rt△BDE中,∠CBF=30°,BD=3,得到DE=
,然后根据AE=AD-DE即可求出AE.
| 3 |
| 3 |
解答:解:∵A,F把半圆三等分,
∴∠ACB=∠CBF=∠ABF=30°,
∴∠BAD=30°,
在Rt△ABC中,BC=12,
所以AB=
BC=6,
在Rt△ABD中,AB=6,
所以BD=
AB=3,AD=
BD=3
,
Rt△BDE中,∠CBF=30°,BD=3,
∴DE=
=
,
∴AE=AD-DE=3
-
=2
.
∴∠ACB=∠CBF=∠ABF=30°,
∴∠BAD=30°,
在Rt△ABC中,BC=12,
所以AB=
| 1 |
| 2 |
在Rt△ABD中,AB=6,
所以BD=
| 1 |
| 2 |
| 3 |
| 3 |
Rt△BDE中,∠CBF=30°,BD=3,
∴DE=
| 3 | ||
|
| 3 |
∴AE=AD-DE=3
| 3 |
| 3 |
| 3 |
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了含30度的直角三角形三边的关系为1:
:2.
| 3 |

练习册系列答案
相关题目
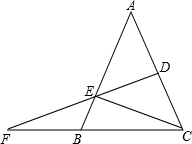 如图,在△ABC中,∠A=45°,边AC的垂直平分线交边AB于E点,交CB的延长线于点F,垂足为点D.如果AB=AC,求证:EC=EF.
如图,在△ABC中,∠A=45°,边AC的垂直平分线交边AB于E点,交CB的延长线于点F,垂足为点D.如果AB=AC,求证:EC=EF.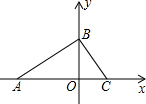 已知:如图,在平面直角坐标系中,点A,B分别在x,y轴上,且OA,OB的长(OA>OB)是一元二次方程x2-7x+12=0的两根.
已知:如图,在平面直角坐标系中,点A,B分别在x,y轴上,且OA,OB的长(OA>OB)是一元二次方程x2-7x+12=0的两根.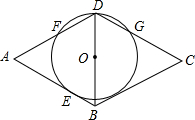 如图,已知O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,与AB、CD分别相交于F、G点.
如图,已知O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,与AB、CD分别相交于F、G点.