题目内容
12. 如图,点A、B、C在⊙O上,∠OBC=18°,则∠A=( )
如图,点A、B、C在⊙O上,∠OBC=18°,则∠A=( )| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
分析 根据圆周角定理可知∠A=$\frac{1}{2}$∠BOC,求出∠BOC的度数即可得出答案.
解答 解:∵OB=OC,
∴∠BOC=180°-2∠OBC=144°,
由圆周角定理可知:∠A=$\frac{1}{2}$∠BOC=72°
故选(C)
点评 本题考查圆周角定理,注意圆的半径都相等,这是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3. 如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
 如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )| A. | 135° | B. | 130° | C. | 120° | D. | 140° |
20.在△ABC中,∠C=90°,AB=5,BC=3,则sinB的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
7.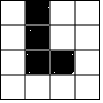 在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有( )
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有( )
 在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有( )
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
17. 有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
 有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,下列结论正确的是( )| A. | a+b<0 | B. | a+b>0 | C. | a-b>0 | D. | b-a=0 |
4.教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛.两人在形同条件下各打了5发子弹,命中环数如下:甲:9、8、7、7、9;乙:10、8、9、7、6.应该选( )参加.
| A. | 甲、乙都可以 | B. | 甲 | C. | 乙 | D. | 无法确定 |
1.下列关于单项式-$\frac{3x{y}^{2}}{5}$的说法中,正确的是( )
| A. | 系数是-$\frac{3}{5}$,次数是2 | B. | 系数是$\frac{3}{5}$,次数是2 | ||
| C. | 系数是-$\frac{3}{5}$,次数是3 | D. | 系数是-3,次数是3 |
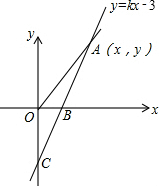 如图,直线y=kx-3与x轴、y轴分别交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别交于B、C两点,且OC=2OB