题目内容
关于x的方程x2+2
x+1=0有两个不相等的实数根,则k= .
| k |
考点:根的判别式
专题:计算题
分析:根据二次根式有意义的条件和判别式的意义得到k≥0且△=(2
)2-4>0,然后求出两个不等式的公共部分即可.
| k |
解答:解:根据题意得k≥0且△=(2
)2-4>0,
解得k>1.
故答案为>1.
| k |
解得k>1.
故答案为>1.
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
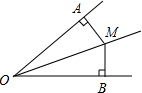 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠MAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠MAB等于( )| A、50°和30° |
| B、40°和70° |
| C、30°和20° |
| D、20°和20° |
若|a|=5,b是-
的倒数,且a<b,则|a+b|等于( )
| 1 |
| 3 |
| A、8 | ||
| B、2 | ||
| C、8或2 | ||
D、5
|
若a,b,c是三角形的三边,则代数式(a-b)2-c2的值是( )
| A、正数 | B、负数 |
| C、等于零 | D、不能确 |