题目内容
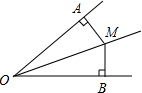 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠MAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠MAB等于( )| A、50°和30° |
| B、40°和70° |
| C、30°和20° |
| D、20°和20° |
考点:角平分线的性质,等腰三角形的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得AM=BM,利用“HL”证明Rt△AOM和Rt△BOM全等,根据全等三角形对应边相等可得OA=OB,再根据等腰三角形两底角相等求出∠OAB,然后求出∠MOB和∠MAB,选择答案即可.
解答: 解:∵OM平分∠AOB,MA⊥OA,MB⊥OB,
解:∵OM平分∠AOB,MA⊥OA,MB⊥OB,
∴AM=BM,
在Rt△AOM和Rt△BOM中,
,
∴Rt△AOM≌Rt△BOM(HL),
∴OA=OB,
∵∠AOB=40°,
∴∠MOB=
×40°=20°,
∠OAB=
(180°-40°)=70°,
∴∠MAB=90°-70°=20°.
故选D.
 解:∵OM平分∠AOB,MA⊥OA,MB⊥OB,
解:∵OM平分∠AOB,MA⊥OA,MB⊥OB,∴AM=BM,
在Rt△AOM和Rt△BOM中,
|
∴Rt△AOM≌Rt△BOM(HL),
∴OA=OB,
∵∠AOB=40°,
∴∠MOB=
| 1 |
| 2 |
∠OAB=
| 1 |
| 2 |
∴∠MAB=90°-70°=20°.
故选D.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,等腰三角形的性质,熟记各性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,厂房屋顶人字架△ABC(等腰三角形),上弦AB=AC,中柱AD(D为底边的中点)中柱AD与BC垂直吗?为什么?
如图,厂房屋顶人字架△ABC(等腰三角形),上弦AB=AC,中柱AD(D为底边的中点)中柱AD与BC垂直吗?为什么?