题目内容
10.化简并求值:$\frac{a-{a}^{2}}{{a}^{2}-1}$÷$\frac{a}{a+1}$•($\frac{a+1}{a-1}$)2,其中a=3.分析 先把各分式的分子分母因式分解,再把除法运算化为乘法运算,然后进行约分得到原式=-$\frac{(a+1)^{2}}{(a-1)^{2}}$,最后把a=3代入计算即可.
解答 解:原式=$\frac{-a(a-1)}{(a+1)(a-1)}$•$\frac{a+1}{a}$•$\frac{(a+1)^{2}}{(a-1)^{2}}$
=-$\frac{(a+1)^{2}}{(a-1)^{2}}$,
当a=3时,原式=-$\frac{(3+1)^{2}}{(3-1)^{2}}$=-4.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
18.下列各式不能用平方差公式的是( )
| A. | (x+y)(x-y) | B. | (x+2y)(2x-y) | C. | (x3+y3)(x3-y3) | D. | (-x-y)(x-y) |
5.已知$\left\{\begin{array}{l}{x-y=3}\\{xy=-3}\end{array}\right.$,则$\frac{5{x}^{2}+10xy+5{y}^{2}}{2x-3xy-2y}$的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
19.代数式a3b2-$\frac{1}{2}$a2b3,$\frac{1}{2}$a3b4+a4b3,a4b2-a2b4的公因式是( )
| A. | a3b2 | B. | a2b2 | C. | a2b3 | D. | a2b4 |
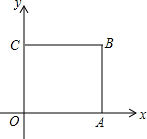 如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.