题目内容
7. 如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为2π.
如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为2π.
分析 首先根据扇形的面积公式求得扇形的半径,然后根据扇形的面积公式S扇形=$\frac{1}{2}$lR(其中l为扇形的弧长),求得扇形的弧长.
解答 解:设扇形的半径是R,则$\frac{60•π•{r}^{2}}{360}$=6π,
解得:r=6,
设扇形的弧长是l,则$\frac{1}{2}$lr=6π,即3l=6π,
解得:l=2π.
故答案是:2π.
点评 本题考查了扇形面积和弧长的计算,熟练掌握扇形的面积公式和弧长的公式是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
17.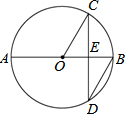 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )| A. | 6 | B. | 5 | C. | 3$\sqrt{3}$ | D. | 3 |
18.下列各式由左到右的变形中,属于分解因式的是( )
| A. | a(m+n)=am+an | B. | a2-b2-c2=(a-b)(a+b)-c2 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+6x=(x+4)(x-4)+6x |
12. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )| A. | 以点F为圆心,OE长为半径画弧 | B. | 以点F为圆心,EF长为半径画弧 | ||
| C. | 以点E为圆心,OE长为半径画弧 | D. | 以点E为圆心,EF长为半径画弧 |
19. 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )
 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )| A. | 100分 | B. | 80分 | C. | 60分 | D. | 40分 |
17.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )


| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
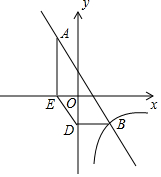 已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.
已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.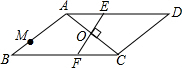 如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.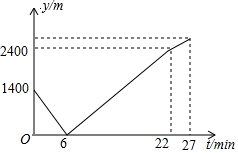 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法: