题目内容
 已知⊙O的半径为5,点O到弦AB的距离OH=3,点P是圆上一动点,设过点P且与AB平行的直线为l,记直线AB到直线l的距离为d.
已知⊙O的半径为5,点O到弦AB的距离OH=3,点P是圆上一动点,设过点P且与AB平行的直线为l,记直线AB到直线l的距离为d.(1)求AB的长;
(2)如果点P只有两个时,求d的取值范围;
(3)如果点P有且只有三个时,求连接这三个点所得到的三角形的面积.
考点:垂径定理,平行线之间的距离
专题:
分析:(1)连接OA,根据勾股定理求出AH,根据垂径定理得出即可;
(2)求出HC和HD的值,结合图形得出即可;
(3)先找出符合条件时的位置,求出三角形的高和底边,根据三角形的面积公式求出即可.
(2)求出HC和HD的值,结合图形得出即可;
(3)先找出符合条件时的位置,求出三角形的高和底边,根据三角形的面积公式求出即可.
解答:解:(1)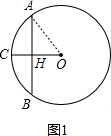
连接OA,如图1,
∵AB⊥OC,
∴∠OHA=90°,AB=2AH,
在Rt△AHO中,OA=5,OH=3,由勾股定理得:AH=4,
∴AB=2AH=8;
(2)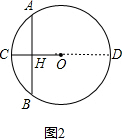
延长CO交⊙O于D,如图2,
∵CH=5-3=2,HD=5+3=8,
∴点P只有两个时d的取值范围是2<d<8;
(3)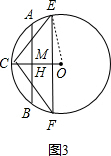
如图3,∵CH=5-3=2,HD=5+3=8,
∴点P有且只有三个时,d=2,
如图,P在C、E、F处,连接OE,
∵OC⊥AB,AB∥EF,
∴OC⊥EF,
∴EF=2EM,
∵OE=5,OM=5-2-2=1,CM=2+2=4,
∴由勾股定理得:EM=
=2
;
∴EF=2EM=4
,
∴S△CEF=
×EF×CM=
×4
×4=8
即点P有且只有三个时,连接这三个点所得到的三角形的面积是8
.

连接OA,如图1,
∵AB⊥OC,
∴∠OHA=90°,AB=2AH,
在Rt△AHO中,OA=5,OH=3,由勾股定理得:AH=4,
∴AB=2AH=8;
(2)

延长CO交⊙O于D,如图2,
∵CH=5-3=2,HD=5+3=8,
∴点P只有两个时d的取值范围是2<d<8;
(3)

如图3,∵CH=5-3=2,HD=5+3=8,
∴点P有且只有三个时,d=2,
如图,P在C、E、F处,连接OE,
∵OC⊥AB,AB∥EF,
∴OC⊥EF,
∴EF=2EM,
∵OE=5,OM=5-2-2=1,CM=2+2=4,
∴由勾股定理得:EM=
| 52-12 |
| 6 |
∴EF=2EM=4
| 6 |
∴S△CEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |
即点P有且只有三个时,连接这三个点所得到的三角形的面积是8
| 6 |
点评:本题考查了垂径定理和勾股定理,直线和圆的位置关系的应用,解此题的关键是能理解题意,题目比较好,但是有一定的难度.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知-32a2mb和b3-na4是同类项,则m+n的值是( )
| A、2 | B、3 | C、4 |
 如图,已知直线y=x+5与反比例函数y=
如图,已知直线y=x+5与反比例函数y=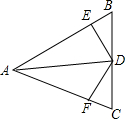 如图,AD平分线∠BAC,AE=AF,则下列说法:①△EAD≌△FAD;②∠AED=∠AFD;③BD=CD;④AD⊥BC.其中正确的有( )
如图,AD平分线∠BAC,AE=AF,则下列说法:①△EAD≌△FAD;②∠AED=∠AFD;③BD=CD;④AD⊥BC.其中正确的有( ) 如图,P、Q为反比例函数图象上的任意两点,过这两点分别向x轴、y轴作垂线,垂足分别为A、B,若S△AOP=2,则S△BOQ=
如图,P、Q为反比例函数图象上的任意两点,过这两点分别向x轴、y轴作垂线,垂足分别为A、B,若S△AOP=2,则S△BOQ=
 如图,P、Q分别为四边形ABCD的边BC,AD上的点,且
如图,P、Q分别为四边形ABCD的边BC,AD上的点,且 如图,l是线段AB的垂直平分线,点P在l上,则PA=
如图,l是线段AB的垂直平分线,点P在l上,则PA=