题目内容
 如图,P、Q分别为四边形ABCD的边BC,AD上的点,且
如图,P、Q分别为四边形ABCD的边BC,AD上的点,且| AQ |
| QD |
| BP |
| PC |
| AB |
| CD |
考点:平行线分线段成比例
专题:证明题
分析:要证明夹角相等,题目中的线段太分散,可以把线段进行集中,如图,将CD平移到C′A的位置,则AC′∥DC,且AC′=DC,过点P作CC′的平行线交BC′于点R,可得到AR平分∠BAC′,再结合条件证明∠BEP=∠BAR=∠RAC′=∠PFC,可得出结论.
解答: 证明:
证明:
如图,将CD平移到C′A的位置,则AC′∥DC,且AC′=DC,
过点P作CC′的平行线交BC′于点R,则BR:RC′=BP:PC=AB:CD=AB:AC,
∴AR平分∠BAC′,
又RP∥CC′,且BP:PC=AQ:QD,
∴RP:CC′=BP:BC=AQ:AD,
而CC′∥AD,且CC′=AD,
∴RP∥AQ,且RP=AQ,
∴AR∥FP,
又AC′∥DC,且AR平分∠BAC′,
∴∠BEP=∠BAR=∠RAC′=∠PFC,
即直线PQ与AB之间的夹角等于直线PQ与CD之间的夹角.
 证明:
证明:如图,将CD平移到C′A的位置,则AC′∥DC,且AC′=DC,
过点P作CC′的平行线交BC′于点R,则BR:RC′=BP:PC=AB:CD=AB:AC,
∴AR平分∠BAC′,
又RP∥CC′,且BP:PC=AQ:QD,
∴RP:CC′=BP:BC=AQ:AD,
而CC′∥AD,且CC′=AD,
∴RP∥AQ,且RP=AQ,
∴AR∥FP,
又AC′∥DC,且AR平分∠BAC′,
∴∠BEP=∠BAR=∠RAC′=∠PFC,
即直线PQ与AB之间的夹角等于直线PQ与CD之间的夹角.
点评:本题主要考查平行线分线段成比例,把题目中的线段集中到一点利用平行得到要求的结论是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
多项式-
+3x+27的次数是( )
| 3xy4 |
| 4 |
| A、7 | B、5 | C、6 | D、13 |
下列运算中正确的是( )
| A、x3•x3=2x6 |
| B、(-x3)2=-x6 |
| C、x5+x=x6 |
| D、(5x)3=125x3 |
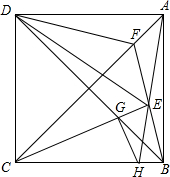 如图,正方形ABCD,以CD为边向正方形内作等边△CDE,连BE交AC于F,连DB交CE与G,连AE并延长交BC于H,连DF,GH.
如图,正方形ABCD,以CD为边向正方形内作等边△CDE,连BE交AC于F,连DB交CE与G,连AE并延长交BC于H,连DF,GH. 已知⊙O的半径为5,点O到弦AB的距离OH=3,点P是圆上一动点,设过点P且与AB平行的直线为l,记直线AB到直线l的距离为d.
已知⊙O的半径为5,点O到弦AB的距离OH=3,点P是圆上一动点,设过点P且与AB平行的直线为l,记直线AB到直线l的距离为d. 如图,点P在∠AOB内部,点M、N分别是点P关于OA、OB的对称点,连接MN,分别交OA、OB于E、F.若MN=8cm,求△PEF的周长.
如图,点P在∠AOB内部,点M、N分别是点P关于OA、OB的对称点,连接MN,分别交OA、OB于E、F.若MN=8cm,求△PEF的周长.