题目内容
8.已知如图:MN∥BC交线段AC于点D,交线段AB于点E,点P为线段AB上异于A,B,E的一点,若∠MDP=α,∠BCP=β.(1)你能用含α、β的式子表示∠CPD的大小吗?请直接写出答案.
(2)请选择以上结论中的任意一个进行证明.

分析 分两种情况进行讨论:①当P在A、E之间时,∠CPD=α-β;②当P在B、E之间时,∠CPD=α+β;先过点P作PF∥MN,再根据平行线的性质,得出∠BCP=∠FPC=α,∠MDP=∠FPD=β,最后根据角的和差关系得出结论.
解答 解:(1)如图,①当P在A、E之间时,∠CPD=α-β;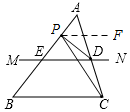
如图,②当P在B、E之间时,∠CPD=α+β;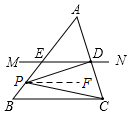
(2)选择①当P在A、E之间时,∠CPD=α-β;
证明:过点P作PF∥MN,则PF∥BC,
∴∠BCP=∠FPC=α,∠MDP=∠FPD=β,
∴∠CPD=∠FPC-∠FPD=∠BCP-∠MDP=α-β;
选择②当P在B、E之间时,∠CPD=α+β;
过点P作PF∥MN,则PF∥BC,
∴∠BCP=∠FPC=α,∠MDP=∠FPD=β,
∴∠CPD=∠FPC+∠FPD=∠BCP+∠MDP=α+β.
点评 本题主要考查了平行线的性质的运用,解决问题的关键是作辅助线,构造平行线,利用两直线平行,内错角相等进行证明.

练习册系列答案
相关题目
 如图:有一个圆柱,底面圆的直径AB=$\frac{16}{π}$,高BC=12,P为BC的中点,蚂蚁从A点爬到P点的最短距离是10.
如图:有一个圆柱,底面圆的直径AB=$\frac{16}{π}$,高BC=12,P为BC的中点,蚂蚁从A点爬到P点的最短距离是10.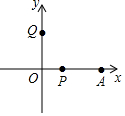 如图,在平面直角坐标系中有一点A,OA=16,动点P从A开始以每秒2个单位的速度向x轴负半轴运动,动点Q从0开始以每秒1个单位的速度向y轴正半轴运动,P,Q同时出发,设时间为t;
如图,在平面直角坐标系中有一点A,OA=16,动点P从A开始以每秒2个单位的速度向x轴负半轴运动,动点Q从0开始以每秒1个单位的速度向y轴正半轴运动,P,Q同时出发,设时间为t; 如图,把数字1,2,3,…,9分别填入图中的9个圈内,要求△ABC和△DEF的每条边上三个圈内的数字之和等于18,给出符合要求的填法.
如图,把数字1,2,3,…,9分别填入图中的9个圈内,要求△ABC和△DEF的每条边上三个圈内的数字之和等于18,给出符合要求的填法.