Question

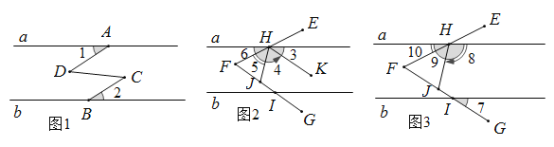
【题目】如图，A、B分别是直线a和b上的点，∠1＝∠2，C、D在两条直线之间，且∠C＝∠D．

（1） 证明：a∥b；

（2） 如图，∠EFG=60°，EF交a于H，FG交b于I，HK∥FG，若∠4＝2∠3，判断∠5、∠6的数量关系，并说明理由；

（3） 如图∠EFG是平角的n分之1（n为大于1的整数），FE交a于H，FG交b于I．点J在FG上，连HJ．若∠8＝n∠7，则∠9：∠10＝______ ．

Answer 1

【答案】（1）见解析；（2），见解析；（3）n-1

【解析】

（1）延长AD交直线b于点E，根据平行线的性质与判定即可得证；

（2）由得到，，再根据三角形的内角和与对顶角的性质即可求解；

（3）延长EF交直线b于点P，过点J作，根据平行线的性质及三角形外角的性质等，得到，，即可得到的值．

（1）如图，延长AD交直线b于点E，

，

，

，

，

，

．

（2）∵，，

∴，，，

∵，

∴，即，

∴，

∵，

∴．

（3）如图，延长EF交直线b于点P，过点J作，

则，，，

∵，，

∴，

，

∴，

故答案为：．