题目内容
14. 在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,则△ABC的面积为30.
在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,则△ABC的面积为30.
分析 先根据点O是△ABC的重心得出OD=$\frac{1}{3}$AD,再由△BOD的面积等于5得出△ABD的面积等于15,再由点D时BC的中点可得出S△ABC=2S△ABD,故可得出结论.
解答 解:∵ABC中,中线AD、BE相交于点O,
∴点O是△ABC的重心,
∴OD=$\frac{1}{3}$AD.
∵S△BOD=5,
∴S△ABD=15.
∵点D时BC的中点,
∴S△ABC=2S△ABD=30.
故答案为:30.
点评 本题考查的是三角形的重心,熟知三角形的重心到顶点的距离与重心到对边中点的距离之比为2:1是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )
把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )
 把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )
把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )| A. | 祝 | B. | 你 | C. | 顺 | D. | 利 |
5.下列实数中,属于有理数的是( )
| A. | $-\sqrt{2}$ | B. | $\root{3}{4}$ | C. | π | D. | $\frac{1}{11}$ |
2.在平面直角坐标系中,点(8,-2)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9. 如图,AB∥CD,以点A为圆心,小于AC长为半径画圆弧,分别交AB、AC于E、F两点:再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径画圆弧,两弧交于点G,作射线AG交CD于点H.若∠C=150°,则∠AHC大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径画圆弧,分别交AB、AC于E、F两点:再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径画圆弧,两弧交于点G,作射线AG交CD于点H.若∠C=150°,则∠AHC大小是( )
 如图,AB∥CD,以点A为圆心,小于AC长为半径画圆弧,分别交AB、AC于E、F两点:再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径画圆弧,两弧交于点G,作射线AG交CD于点H.若∠C=150°,则∠AHC大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径画圆弧,分别交AB、AC于E、F两点:再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径画圆弧,两弧交于点G,作射线AG交CD于点H.若∠C=150°,则∠AHC大小是( )| A. | 15° | B. | 25° | C. | 30° | D. | 35° |
19. 如图,把一块等腰直角三角板的锐角顶点放在直尺的一边上,如果∠1=20°,那么这个锐角所对的直角边与直尺的另一边相交所得的∠2的度数是( )
如图,把一块等腰直角三角板的锐角顶点放在直尺的一边上,如果∠1=20°,那么这个锐角所对的直角边与直尺的另一边相交所得的∠2的度数是( )
 如图,把一块等腰直角三角板的锐角顶点放在直尺的一边上,如果∠1=20°,那么这个锐角所对的直角边与直尺的另一边相交所得的∠2的度数是( )
如图,把一块等腰直角三角板的锐角顶点放在直尺的一边上,如果∠1=20°,那么这个锐角所对的直角边与直尺的另一边相交所得的∠2的度数是( )| A. | 60° | B. | 65° | C. | 70° | D. | 80° |
6. 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{11}{4}$ | D. | $\frac{\sqrt{26}}{2}$ |
 甲、乙两人骑车分别从A,B两地同时出发,相向而行.两人从出发到相遇共用了6小时,而且两人在此过程中,均改变了一次骑车速度.其中两人行驶路程y(km)与行驶时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD,如图所示,
甲、乙两人骑车分别从A,B两地同时出发,相向而行.两人从出发到相遇共用了6小时,而且两人在此过程中,均改变了一次骑车速度.其中两人行驶路程y(km)与行驶时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD,如图所示,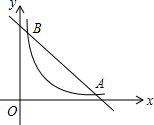 如图,在直角坐标系中,直线y=6-x与双曲线$y=\frac{4}{x}$ (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为4,12.
如图,在直角坐标系中,直线y=6-x与双曲线$y=\frac{4}{x}$ (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为4,12.