题目内容
10.把下列各式分母有理化:(1)$\frac{a-b}{\sqrt{a}+\sqrt{b}}(a≠b)$
(2)$\frac{\sqrt{a+2}-\sqrt{a-2}}{\sqrt{a+2}+\sqrt{a-2}}$
(3)$\frac{b-\sqrt{{a}^{2}+{b}^{2}}}{b+\sqrt{{a}^{2}+{b}^{2}}}$.
分析 (1)先分子和分母都乘以分母的有理化因式,再化简即可;
(2)先分子和分母都乘以分母的有理化因式,再化简即可;
(3)先分子和分母都乘以分母的有理化因式,再化简即可.
解答 解:(1)原式=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$
=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{a-b}$
=$\sqrt{a}$-$\sqrt{b}$;
(2)原式=$\frac{(\sqrt{a+2}-{\sqrt{a-2})}^{2}}{(\sqrt{a+2}+\sqrt{a-2})(\sqrt{a+2}-\sqrt{a-2})}$
=$\frac{a+2-2\sqrt{{a}^{2}-4}+a-2}{(a+2)-(a-2)}$
=$\frac{a-\sqrt{{a}^{2}-4}}{2}$;
(3)原式=$\frac{(b-\sqrt{{a}^{2}+{b}^{2}})^{2}}{(b+\sqrt{{a}^{2}+{b}^{2}})(b-\sqrt{{a}^{2}+{b}^{2}})}$
=$\frac{{b}^{2}-2b\sqrt{{a}^{2}+{b}^{2}}+{a}^{2}+{b}^{2}}{{b}^{2}-({a}^{2}+{b}^{2})}$
=-$\frac{2{b}^{2}+{a}^{2}-2b\sqrt{{a}^{2}+{b}^{2}}}{{a}^{2}}$.
点评 本题考查分母有理化的应用,能知道分母的有理化因式是解此题的关键,难度适中.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.若等腰△ABC的两边长分别是4和7,则其周长为( )
| A. | 14 | B. | 15 | C. | 18 | D. | 15或18 |
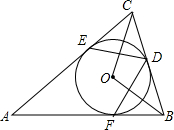 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.