题目内容
18.一般地,抛物线y=ax2+bx+c通过配方可得y=a(x+$\frac{b}{2a}$)2+$\frac{4ac-{b}^{2}}{4a}$,所以抛物线y=ax2+bx+c的对称轴是直线-$\frac{b}{2a}$,顶点坐标是($\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).分析 利用完全平方公式的结构,将二次函数配方后即可得到答案.
解答 解:∵y=ax2+bx+c=a(x+$\frac{b}{2a}$)2+$\frac{4ac-{b}^{2}}{4a}$,
∴对称轴是x=-$\frac{b}{2a}$,顶点坐标是($\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
故答案为:$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$,-$\frac{b}{2a}$,($\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).
点评 本题考查了二次函数的性质,牢记其顶点坐标公式是解决二次函数的有关知识的基础.

练习册系列答案
相关题目
6.我县某初中七年级进行了一次数学测验,参加人数共540人,为了了解这次数学测验成绩,下列所抽取的样本中较为合理的是( )
| A. | 抽取前100名同学的数学成绩 | |
| B. | 抽取后100名同学的数学成绩 | |
| C. | 抽取(1)(2)两班同学的数学成绩 | |
| D. | 抽取各班学号为6号的倍数的同学的数学成绩 |

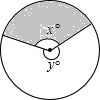 如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为多少?(精确到0.1)
如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为多少?(精确到0.1)