题目内容
 如图,△ABC中,∠B=2∠C,AD为BC边上的高,点E为BC的中点.求证:DE=
如图,△ABC中,∠B=2∠C,AD为BC边上的高,点E为BC的中点.求证:DE=| 1 |
| 2 |
考点:直角三角形斜边上的中线,等腰三角形的判定与性质,三角形中位线定理
专题:证明题
分析:取AC的中点F,连接EF、DF,根据直角三角形斜边上的中线等于斜边的一半可得CF=DF,根据等边对等角可得∠CDF=∠C,根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AB,EF=
AB,根据两直线平行,同位角相等可得∠CEF=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CDF=∠DFE,再根据等角对等边可得EF=DE,从而得证.
| 1 |
| 2 |
解答: 证明:如图,取AC的中点F,连接EF、DF,
证明:如图,取AC的中点F,连接EF、DF,
∵AD为BC边上的高,
∴CF=DF,
∴∠CDF=∠C,
∵点E为BC的中点,
∴EF是△ABC的中位线,
∴EF∥AB,EF=
AB,
∴∠CEF=∠B,
由三角形的外角性质,∠CEF=∠CDF+∠DFE,
∵∠B=2∠C,
∴∠CDF+∠DFE=2∠CDF,
∴∠CDF=∠DFE,
∴EF=DE,
∴DE=
AB.
 证明:如图,取AC的中点F,连接EF、DF,
证明:如图,取AC的中点F,连接EF、DF,∵AD为BC边上的高,
∴CF=DF,
∴∠CDF=∠C,
∵点E为BC的中点,
∴EF是△ABC的中位线,
∴EF∥AB,EF=
| 1 |
| 2 |
∴∠CEF=∠B,
由三角形的外角性质,∠CEF=∠CDF+∠DFE,
∵∠B=2∠C,
∴∠CDF+∠DFE=2∠CDF,
∴∠CDF=∠DFE,
∴EF=DE,
∴DE=
| 1 |
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,三角形的中位线平行于第三边并且等于第三边的一半,等角对等边和等边对等角的性质,熟记各性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
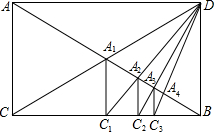 如图,对于任意线段AB,可以构造以AB为对角线的矩形ACBD.连接CD,与AB交于A1点,过A1作BC的垂线段A1C1,垂足为C1;连接C1D,与AB交于A2点,过A2作BC的垂线段A2C2,垂足为C2;连接C2D,与AB交于A3点,过A3作BC的垂线段A3C3,垂足为C3…如此下去,可以依次得到点A4,A5,…,An.如果设AB的长为1,依次可求得A1B,A2B,A3B…的长,则AnB的长为(用n的代数式表示)( )
如图,对于任意线段AB,可以构造以AB为对角线的矩形ACBD.连接CD,与AB交于A1点,过A1作BC的垂线段A1C1,垂足为C1;连接C1D,与AB交于A2点,过A2作BC的垂线段A2C2,垂足为C2;连接C2D,与AB交于A3点,过A3作BC的垂线段A3C3,垂足为C3…如此下去,可以依次得到点A4,A5,…,An.如果设AB的长为1,依次可求得A1B,A2B,A3B…的长,则AnB的长为(用n的代数式表示)( )
 在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E.
在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E.