题目内容
11.等边△ABC的边长为2,P是平面内任意一点,△PAB、△PBC、△PAC均为等腰三角形.(1)请用尺规作图的方法作出所有满足条件的点P(不写做法,保留作图痕迹,用P1,P2,P3…表示);
(2)直接写出∠PAB的度数;
(3)在满足条件的所有点P中任取2点,则这两点距离的最小值是2-$\frac{2\sqrt{3}}{3}$,最大值是2+2$\sqrt{3}$.
分析 (1)根据等腰三角形定义分别以A、B、C为圆心,AB为半径画弧即可得到所求的点P.
(2)根据等边三角形的性质以及内角和定理即可得出∠PAB.
(3)利用图象观察即可得出最小值P1P2以及最大值P5P10,根据特殊角时间函数即可求出.
解答 解:(1)如图所示满足条件的点P有10个.
(2)∠PAB=15°或30°或60°或75°或120°或150°.
(3)在RT△P1BH中,∵BH=1,∠HBP1=30°,
∴BP1=$\frac{2\sqrt{3}}{3}$,
∴最小值P1P2=BP2-BP1=AB-BP1=2-$\frac{2\sqrt{3}}{3}$,
∴最大值P5P10=P5H+HC+CP10=2HC+AC=2+2$\sqrt{3}$,
故答案为:,2-$\frac{2\sqrt{3}}{3}$;2+2$\sqrt{3}$.
点评 此题考查图形与作图问题,熟练掌握等边三角形的性质及等腰三角形的判定是解题关键,记住一些常用结论等边三角形的高=$\frac{\sqrt{3}}{2}$a(a是边长).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.
(1)在给出的直角坐标系内用描点法画出该二次函数的图象;
(2)根据所画的函数图象写出当x在什么范围内时,y≤0?
(3)根据所画的函数图象写出方程:x2-4x=5的解.
 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.(1)在给出的直角坐标系内用描点法画出该二次函数的图象;
(2)根据所画的函数图象写出当x在什么范围内时,y≤0?
(3)根据所画的函数图象写出方程:x2-4x=5的解.
3.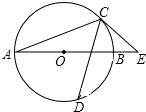 如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
 如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
