题目内容
3.下列因式分解正确的是( )| A. | ax2-ay2=a(x2+y2) | B. | x2+2x+1=x(x+2)+1 | C. | (x+y)(x-y)=x2-y2 | D. | x2+4x+4=(x+2)2 |
分析 原式各项利用提取公因式,平方差公式及完全平方公式分解得到结果,即可作出判断.
解答 解:A、原式=a(x+y)(x-y),错误;
B、原式=(x+1)2,错误;
C、原式为最简结果,错误;
D、原式=(x+2)2,正确,
故选D
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.化简(2-2a)2-(-2a)2的结果是( )
| A. | 0 | B. | 2a2 | C. | -6a2 | D. | 4-8a |
18.下列分解因式正确的是( )
| A. | 2x2-4x=x(2x-4) | B. | x2-1=(x+1)(x-1) | C. | x2-x+2=x(x-1)+2 | D. | x2+2x-1=(x-1)2 |
8.为执行“两免一补”政策,某地区2014年投入教育经费2500万元,预计到2016年,三年共投入8275万元.设投入教育经费的年平均增长率为x,那么下列方程正确的是( )
| A. | 2500x2=8275 | B. | 2500(1+x%)2=8275 | ||
| C. | 2500(1+x)2=8275 | D. | 2500+2500(1+x)+2500(1+x)2=8275 |
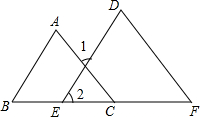 如图填空:
如图填空: 已知:如图,O点在△ABC内部,连AO、BO、CO,A′、B′、C′分别在AO、BO、CO上,且AB∥A′B′、BC∥B′C′.图中△OAC与△OA′C′相似吗?为什么?
已知:如图,O点在△ABC内部,连AO、BO、CO,A′、B′、C′分别在AO、BO、CO上,且AB∥A′B′、BC∥B′C′.图中△OAC与△OA′C′相似吗?为什么?