题目内容
7.对于任意两个实数对(a,b)和(c,d),规定:当且仅当a=c且b=d时,(a,b)=(c,d),定义运算“⊕”:(a,b)⊕(c,d)=(ac-bd,ad+bc),若(2,3)⊕(p,q)=(4,32),则p和q的值是9,$\frac{14}{3}$.分析 根据题意将原式变形得出关于p,q的方程组,进而得出答案.
解答 解:∵(2,3)⊕(p,q)=(4,32),
∴(2p-3q,2q+3p)=(4,32),
∴$\left\{\begin{array}{l}{2q-3p=4}\\{2q+3p=32}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{q=9}\\{p=\frac{14}{3}}\end{array}\right.$,
故p=$\frac{14}{3}$,q=9.
故答案为:9,$\frac{14}{3}$.
点评 此题主要考查了实数运算,正确将原式变形得出p,q的方程组是解题关键.

练习册系列答案
相关题目
2.三角形三边长分别为15、20、25,则最短边上的高为( )
| A. | 15 | B. | 20 | C. | 24 | D. | 25 |
12.某玻璃制品销售公司职工的月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售件数),如表是甲、乙两位职工某月的工资情况.
(1)求职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 200 | 180 |
| 月工资(元) | 1800 | 1700 |
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
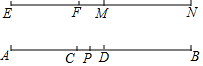 如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )
如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )