题目内容
3. 如图,直线l过正方形ABCD的顶点B,A、C两顶点在直线l两侧,过点A、C分别作AE⊥直线l,CF⊥直线l,垂足分别为E、F.求证:EF=AE-CF.
如图,直线l过正方形ABCD的顶点B,A、C两顶点在直线l两侧,过点A、C分别作AE⊥直线l,CF⊥直线l,垂足分别为E、F.求证:EF=AE-CF.
分析 先利用AAS判定△ABE≌△BCF,从而得出AE=BF,BE=CF,最后得出EF=AE-CF.
解答 解:∵四边形ABCD是正方形,
∴∠CBF+∠FBA=90°,AB=BC,
∵CF⊥BE,
∴∠CBF+∠BCF=90°,
∴∠BCF=∠ABE,
∵∠AEB=∠BFC=90°,AB=BC,
∴△ABE≌△BCF(AAS)
∴AE=BF,BE=CF,
∴AE-CF=BF-BE=EF,
即:EF=AE-CF.
点评 此题主要考查了正方形的性质及全等三角形的判定方法,做题时要注意各个条件之间的关系并灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.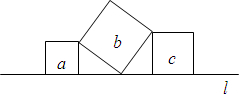 如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )
如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )
 如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )
如图,直线l上有三个正方形a、b、c,若a、c的边长分别为1和2,则b的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.已知a>b,则下列不等关系中,正确的是( )
| A. | ac>bc | B. | a+c2>b+c2 | C. | a-1>b+1 | D. | ac2>bc2 |
 如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于M,交AB于N,若AC=8,MB=2MC,求AB的长.
如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于M,交AB于N,若AC=8,MB=2MC,求AB的长. 如图直线l经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BE⊥l于点E,DF⊥l于点F.以正方形对角线的交点O为端点,引两条相互垂直的射线分别与AD、CD交于G、H两点,若EF=2,S△ABE=$\frac{1}{2}$,则线段GH长度的最小值是1.
如图直线l经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BE⊥l于点E,DF⊥l于点F.以正方形对角线的交点O为端点,引两条相互垂直的射线分别与AD、CD交于G、H两点,若EF=2,S△ABE=$\frac{1}{2}$,则线段GH长度的最小值是1.