已知等腰三角形的两边长分别为2.7.则它的周长为16．题目和参考答案——青夏教育精英家教网——

题目内容

11．已知等腰三角形的两边长分别为2、7，则它的周长为16．

分析根据2和7可分别作等腰三角形的腰，结合三边关系定理，分别讨论求解．

解答解：当2为腰时，三边为2，2，7，由三角形三边关系定理可知，不能构成三角形，
当7为腰时，三边为7，7，2，符合三角形三边关系定理，周长为：7+7+2=16．
故答案为：16．

点评本题考查了等腰三角形的性质，三角形三边关系定理．关键是根据2，7，分别作为腰，由三边关系定理，分类讨论．

练习册系列答案

课堂制胜课时作业系列答案

名师计划高效课堂系列答案

练习新方案系列答案

新评价单元检测创新评价系列答案

新课标单元测试卷系列答案

形成性练习与检测系列答案

形成性自主评价系列答案

南方新课堂金牌学案系列答案

挑战100单元检测试卷系列答案

金版新学案系列答案

相关题目

1．若点P（a，a-2）在第四象限，则a的取值不能是（　　）

2．我们知道用几何图形的面积可以解释多项式乘法的运算：
（1）如图1，可知：（a+b）²=a²+2ab+b²；
（2）如图2，可知：（a+b）²=（a-b）²+4ab；
（3）计算：（a+b）（a+2b）=a²+3ab+2b²；
（4）在下面虚线框内画图说明（3）中的等式．

19．在π，$\sqrt{3}$，1.732，3.14四个数中，无理数的个数是（　　）

6．直线y=kx+b交坐标轴于A（-2，0），B（0，3）两点，求不等式kx+b＞0的解集．

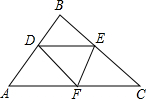如图，在△ABC中，AB，BC，CA的长分别为6，7，8，且D，E，F分别是AB，BC，CA的中点，依次连接D，E，F得到△DEF，则△DEF的周长为10.5．

一次越野跑中，当小明跑了1600米时，小刚跑了1400米，小明、小刚在此后所跑的路程y（米）与时间t（秒）之间的函数关系如图所示，则这次越野跑的全程为2200米．

2．用科学记数法表示下列各数．
（1）0.003009；
（2）-0.00001096；
（3）0.000329．

如图，直线l过正方形ABCD的顶点B，A、C两顶点在直线l两侧，过点A、C分别作AE⊥直线l，CF⊥直线l，垂足分别为E、F．求证：EF=AE-CF．