题目内容
20．已知a+1的平方根是±2，3a-b-6的立方根是-2．则a+2b的算术平方根为5．分析 先根据平方根，立方根的定义列出关于a、b的二元一次方程组，再代入进行计算求a+2b的值，然后根据算术平方根的定义求解．
解答 解：根据题意得：$\left\{\begin{array}{l}{a+1=（±2）^{2}}\\{3a-b-6=（-2）^{3}}\end{array}\right.$．
解得：$\left\{\begin{array}{l}{a=3}\\{b=11}\end{array}\right.$．
a+2b=3+22=25，
25的算术平方根是5．
故答案为：5．
点评 本题考查了平方根，立方根，算术平方根的定义，列式求出a、b的值是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11．要使$\frac{\sqrt{x-4}}{x-5}$有意义，则x的取值范围是（ ）
| A． | x＞4 | B． | x≠5 | C． | x≥4且x≠5 | D． | x≠5 |
8．如表：方程1、方程2、方程3…是按照一定规律排列的一列方程：
（1）若方程$\frac{a}{x}$-$\frac{1}{x-b}$=1（a＞b）的解是x1=6，x2=10，则a=12b=5．
（2）请写出这列方程中第n个方程：$\frac{2n+4}{x}-\frac{1}{x-（n+1）}=1$ 方程的解：x1=n+2，x2=2n+2．
| 序号 | 方程 | 方程的解 |
| 1 | $\frac{6}{x}$-$\frac{1}{x-2}$=1 | x1=3，x2=4 |
| 2 | $\frac{8}{x}$-$\frac{1}{x-3}$=1 | x1=4，x2=6 |
| 3 | $\frac{10}{x}$-$\frac{1}{x-4}$=1 | x1=5，x2=8 |
| … | … | … |
（2）请写出这列方程中第n个方程：$\frac{2n+4}{x}-\frac{1}{x-（n+1）}=1$ 方程的解：x1=n+2，x2=2n+2．
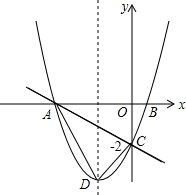已知抛物线y=ax2+bx+c与x轴交于A、B两点，交y轴于点C，点D为顶点且△ABC的是直角三角形，A点坐标为（-4，0），C点的坐标为（0，-2），直线y=kx+b经过A、C两点．