题目内容
13.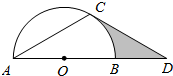 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积.
分析 (1)连接OC,易证∠A=∠D=30°,由于OA=OC,所以∠ACO=∠A=30°,从而可知∠OCD=90°,即OC⊥CD.
(2)分别求出扇形BOC与直角三角形OCD的面积即可求出阴影部分面积.
解答 解:连接OC,
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°,
∵OA=OC,
∴∠ACO=∠A=30°,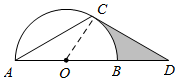
∴∠COD=60°
∴∠OCD=180°-∠COD-∠D=90°
∴OC⊥CD
∴CD是⊙O的切线;
(2)由(1)可知:∠COD=60°,
∴S扇形BOC=$\frac{60π×{4}^{2}}{360}$=$\frac{8π}{3}$
在Rt△OCD中,
tan60°=$\frac{CD}{OC}$
∴CD=4$\sqrt{3}$,
∴S△OCD=$\frac{1}{2}$OC×CD=8$\sqrt{3}$,
∴阴影部分面积为:8$\sqrt{3}$-$\frac{8π}{3}$
点评 本题考查圆的综合问题,涉及切线的判定,扇形的面积公式,锐角三角函数等知识,综合程度较高,属于中等题型.

练习册系列答案
相关题目
8. 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n,2n-1) | C. | (2n-1,2n+1) | D. | (2n-1,2n) |
5.王红在做一道双选择题(即有两个选项是正确的)时,发现四个选项都有可能正确,于是她从中任选两个,那么她做对此题的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2.2017年4月20日19时41分,中国自主研制的首个货运飞船“天舟一号”,搭载“长征七号”火箭在海南省文昌航天发射场发射成功,被称为“太空快递小哥”的“天舟一号”,起飞重量约13吨,将13吨用科学记数法可表示为( )
| A. | 13×103千克 | B. | 1.3×103千克 | C. | 1.3×104千克 | D. | 1.3×105千克 |
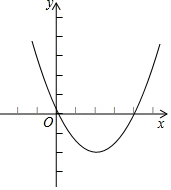 在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).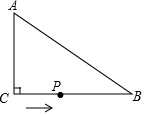 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.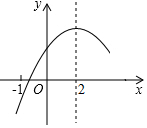 二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(-1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(-1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )