题目内容
18. 如图,将宽为1cm的纸条沿AC折叠,使∠ABC=60°,则折叠后重叠部分三角形的周长为( )
如图,将宽为1cm的纸条沿AC折叠,使∠ABC=60°,则折叠后重叠部分三角形的周长为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 根据翻折的性质可得∠1=∠2,根据两直线平行,内错角相等可得∠1=∠3,从而得到∠2=∠3,再判断出△ABC是等边三角形,然后根据等边三角形的性质求出边长,然后求解即可.
解答  解:如图,由翻折得,∠1=∠2,
解:如图,由翻折得,∠1=∠2,
∵纸条对边互相平行,
∴∠1=∠3,
∴∠2=∠3,
∵∠ABC=60°,
∴△ABC是等边三角形,
∵纸条宽度为1cm,
∴等边三角形的边长=1÷$\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{3}$,
∴折叠后重叠部分三角形的周长=3×$\frac{2\sqrt{3}}{3}$=2$\sqrt{3}$.
故选B.
点评 本题考查了翻折变换的性质,等边三角形的判定与性质,翻折前后对应角相等,对应边相等,本题判断出等边三角形是解题的关键.

练习册系列答案
相关题目
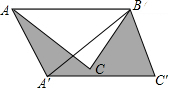 如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2.
如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2. 己知:直线y=x+3与x轴、y轴分别交于点A、B,抛物线y=ax2+bx+c(a、b、c均不为0)与x轴交于点C、D两点.
己知:直线y=x+3与x轴、y轴分别交于点A、B,抛物线y=ax2+bx+c(a、b、c均不为0)与x轴交于点C、D两点.