Question

城市规划期间，欲拆除一电线杆AB，如图，已知距电线杆AB的水平距离14m的D处有一大坝，背水坡CD的坡度i=2：1，坝高CF为2m，在坝顶点C处测得电线杆顶点A的仰角为30°，DE之间是宽为2m的行人道，试问在拆除电线杆AB时，为确保行人安全，______将此人行道封上．（请填“需要”或“不需要”，提示：在地面上，以点B为圆心，以AB为半径的圆形区域为危险区域）

Answer 1

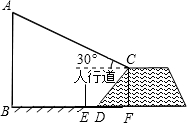
如图，作CM⊥AB于点M，则MBFC为矩形．
∴BM=CF=2，BF=CM
∵背水坡CD的坡度为i=2：1，
∴

CF

DF

=

2

1

，∴DF=

1

2

CF=1．
∴CM=BF=BD+DF=14+1=15．
在Rt△AMC中，∵tan∠ACM=

AM

CM

，
∴AM=CM•tan∠ACM=15•tan30°=15×

3

3

=5

3

．
∴AB=AM+BM=5

3

+2≈10.66（m）．
而BE=BD-DE=14-2=12（m）．
∴AB＜BE．故不需封闭人行道DE．