题目内容
如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1

(1)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(2)在(1)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)

(1)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(2)在(1)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)
考点:图形的剪拼
专题:
分析:(1)由全等三角形的性质就可以得出△BC1C与△BA1A是等腰三角形,且∠C1BC=∠A1BA,就可以求出∠3=∠C1A1B,就可以得出结论;
(2)通过∠A1C1C=∠A1BC就可以得出∠BFC1=∠BC1A1,就可以得出△BFC1∽△BC1A1,就可以得出
=
,进而就可以求出结论.
(2)通过∠A1C1C=∠A1BC就可以得出∠BFC1=∠BC1A1,就可以得出△BFC1∽△BC1A1,就可以得出
| C1F |
| C1A1 |
| BC1 |
| BA1 |
解答:解:(1)∠A1C1C=∠A1BC.
理由:∵△ABC≌△A1B1C1,
∴BC1=BC,BA1=BA,∠1=∠2,∠A=∠C1A1B.
∴∠1+∠4=∠2+∠4,∠3=∠5,∠A=∠C1A1B,
∴∠C1BC=∠A1BA.
∵∠C1BC+2∠3=∠A1BA+2∠A=180°,
∴∠3=∠A,
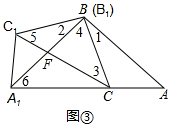
∴∠3=∠C1A1B.
∵∠C1FA1=∠CFB
∴∠A1C1C=∠A1BC;
(2)∵∠A1C1C=∠A1BC,
∴∠A1C1C+∠5=∠A1BC+∠3,
∴∠A1C1B=∠A1BC+∠3.
∵∠BFC1=∠A1BC+∠3.
∴∠A1C1B=∠BFC1.
∵∠2=∠2,
∴△BFC1∽△BC1A1,
∴
=
,
∴
=
,
∴y=
.
理由:∵△ABC≌△A1B1C1,
∴BC1=BC,BA1=BA,∠1=∠2,∠A=∠C1A1B.
∴∠1+∠4=∠2+∠4,∠3=∠5,∠A=∠C1A1B,
∴∠C1BC=∠A1BA.
∵∠C1BC+2∠3=∠A1BA+2∠A=180°,
∴∠3=∠A,

∴∠3=∠C1A1B.
∵∠C1FA1=∠CFB
∴∠A1C1C=∠A1BC;
(2)∵∠A1C1C=∠A1BC,
∴∠A1C1C+∠5=∠A1BC+∠3,
∴∠A1C1B=∠A1BC+∠3.
∵∠BFC1=∠A1BC+∠3.
∴∠A1C1B=∠BFC1.
∵∠2=∠2,
∴△BFC1∽△BC1A1,
∴
| C1F |
| C1A1 |
| BC1 |
| BA1 |
∴
| y |
| 3 |
| 6 |
| x |
∴y=
| 18 |
| x |
点评:本题考查了全等三角形的性质的运用,等腰三角形的判定及性质的运用,相似三角形的判定及性质的运用,题目的综合性较强,难度较大.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,若AB=CD=4,则梯形ABCD的周长为( )
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,若AB=CD=4,则梯形ABCD的周长为( )| A、16 | ||
| B、18 | ||
| C、20 | ||
D、12+4
|
两数-3
,2
的和比它们的相反数的和小( )
| 1 |
| 2 |
| 1 |
| 3 |
A、2
| ||
B、-2
| ||
C、1
| ||
D、-
|
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AB⊥AC.设∠ACB=x°.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AB⊥AC.设∠ACB=x°. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数.
如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,求∠BAB′的度数. 小明同学的座右铭是“细节决定成败”,他将这几个字写在一个正方体纸盒的每个面上,其表面展开图如图所示,那么在该正方体中,和“细”相对的字是( )
小明同学的座右铭是“细节决定成败”,他将这几个字写在一个正方体纸盒的每个面上,其表面展开图如图所示,那么在该正方体中,和“细”相对的字是( )