题目内容
 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=18,CD=21,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为
把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=18,CD=21,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为考点:旋转的性质
专题:
分析:由旋转的性质可得到O为AB中点,可求得OA,OD1,利用勾股定理可求得AD1.
解答:解:∵∠BCE=15°,∠D1CE=∠DCE=60°,
∴∠D1CB=∠D1CE-∠BCE=45°,
∵AC=BC,∠ACB=90°,
∴AO=BO=CO=
AB=9,
∴DO=CD-CO=21-9=12,
在Rt△AOD1中由勾股定理可求得AD1=15.
故答案为:15.
∴∠D1CB=∠D1CE-∠BCE=45°,
∵AC=BC,∠ACB=90°,
∴AO=BO=CO=
| 1 |
| 2 |
∴DO=CD-CO=21-9=12,
在Rt△AOD1中由勾股定理可求得AD1=15.
故答案为:15.
点评:本题主要考查旋转的性质及直角三角形的性质,掌握旋转图形为全等图形是解题的关键.注意勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积为1.44m2?(设窗框宽为xm )
用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积为1.44m2?(设窗框宽为xm )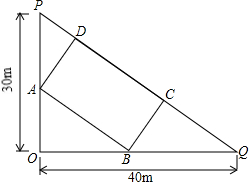 如图所示,直角三角形内部有一矩形,求矩形的最大面积.
如图所示,直角三角形内部有一矩形,求矩形的最大面积. 已知AB是⊙O的直径,在OA上取一点M,作MC、MD与⊙O分别交于C、D两点,且∠BMC=∠BMD.求证:MC=MD.
已知AB是⊙O的直径,在OA上取一点M,作MC、MD与⊙O分别交于C、D两点,且∠BMC=∠BMD.求证:MC=MD.