题目内容
5.已知x=-2,求代数式(2x-y)(2x+y)+(2x-y)(y-4x)+2y(y-3x)的值,在解这道题时,小红说:“只给出了x的值,没给出y的值,求不出答案.”小丽说:“这道题与y的值无关,不给出y的值,也能求出答案.”(1)你认为谁的说法正确?请说明理由.
(2)如果小红的说法正确,那么你给出一个合适的y的值求出这个代数式的值,如果小丽的说法正确,那么请你直接求出这个代数式的值.
分析 (1)先算乘法,再合并同类项,即可得出答案;
(2)把x=-2代入求出即可.
解答 解:(1)小丽的说法正确,理由如下:
原式=4x2-y2-(8x2-6xy+y2)+2y2-6xy
=4x2-y2-8x2+6xy-y2+2y2-6xy
=-4x2,
化简后y消掉了,所以代数式的值与y无关.所以小丽的说法正确;
(2)当x=-2时,原式=-4×(-2)2=-16,
即这个代数式的值是-16.
点评 本题考查了整式的混合运算和求值的应用,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
16. 如图,在矩形ABCD中,对角线AC和BD交于点O,若OB=4,则BD的长为( )
如图,在矩形ABCD中,对角线AC和BD交于点O,若OB=4,则BD的长为( )
 如图,在矩形ABCD中,对角线AC和BD交于点O,若OB=4,则BD的长为( )
如图,在矩形ABCD中,对角线AC和BD交于点O,若OB=4,则BD的长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
20.若x-$\frac{1}{x}$=3,则x2+$\frac{1}{{x}^{2}}$的值为( )
| A. | 3 | B. | -11 | C. | 11 | D. | -3 |
10.下列说法不正确的是( )
| A. | 能够完全重合的两个图形是全等形 | |
| B. | 形状相同的两个图形是全等形 | |
| C. | 大小不同的两个图形不是全等形 | |
| D. | 形状、大小都相同的两个图形是全等形 |
17.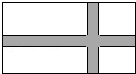 如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.设小路的宽为x,则可列方程为( )
如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.设小路的宽为x,则可列方程为( )
 如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.设小路的宽为x,则可列方程为( )
如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.设小路的宽为x,则可列方程为( )| A. | (40-2x)(32-x)=1140 | B. | (40-x)(32-x)=1140 | C. | (40-x)(32-2x)=1140 | D. | (40-2x)(32-2x)=1140 |
14.如果直角三角形的三边长是3,5,a,那么a的取值可以有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.若一个多边形的每一个外角都是60°,则这个多边形的内角和为( )
| A. | 1080° | B. | 180° | C. | 360° | D. | 720° |