题目内容
10.已知函数y=mx2-3(m-1)x+2m-3(1)求证:无论m取任何实数时,函数与x轴总有交点;
(2)若函数y=mx2-3(m-1)x+2m-3的图象关于y轴对称,求m的值.
分析 (1)根据题意,若函数是一次函数,则二次项系数为0即可;若函数是二次函数,则只要证明判别式△=b2-4ac恒大于0即可;
(2)根据二次函数的解析式对称轴为y轴可得,对称轴为x=-$\frac{b}{2a}$=0,即可求得m的值.
解答 (1)证明:当m=0时,原方程可化为3x-3=0,解得x=1;
当m≠0时,
∵△=[-3(m-1)]2-4×m×(2m-3)=m2-6m+9=(m-3)2≥0,
∴无论m取任何实数时,方程总有实数根;
(2)解:∵关于x的二次函数y1=mx2-3(m-1)x+2m-3的图象关于y轴对称,
∴对称轴:x=$-\frac{b}{2a}=-\frac{-3(m-1)}{2m}=0$,
即:3(m-1)=0,
解得:m=1.
点评 此题考查了一元二次方程根的情况以及待定系数法求二次函数的解析式.第(1)小题中,明确函数可能是一次函数也可能是二次函数,注意分类讨论思想的应用是解决此题的关键;第(2)小题,熟记二次函数的对称轴是解决此题的关键,注意掌握方程思想的应用.

练习册系列答案
相关题目
20.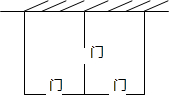 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )| A. | 75m2 | B. | $\frac{75}{2}{m}^{2}$ | C. | 48m2 | D. | $\frac{225}{2}{m}^{2}$ |
1.下列说法正确的是( )
| A. | 任意三点可以确定一个圆 | |
| B. | 平分弦的直径垂直于弦,并且平分该弦所对的弧 | |
| C. | 同一平面内,点P到⊙O上一点的最小距离为2,最大距离为8,则该圆的半径为5 | |
| D. | 同一平面内,点P到圆心O的距离为5,且圆的半径为10,则过点P且长度为整数的弦共有5条 |
5.下列函数中,是二次函数的是( )
| A. | y=ax2+bx+c | B. | y=(x+2)(x-2)-x2 | C. | $y=\sqrt{{x^2}-2x+1}$ | D. | $y=\frac{1}{2}({x-3})x$ |
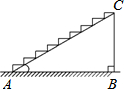 如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.
如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.