题目内容
20.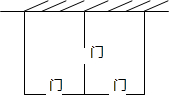 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )| A. | 75m2 | B. | $\frac{75}{2}{m}^{2}$ | C. | 48m2 | D. | $\frac{225}{2}{m}^{2}$ |
分析 设垂直于墙的材料长为x米,则平行于墙的材料长为27+3-3x=30-3x,表示出总面积S=x(30-3x)=-3x2+30x=-3(x-5)2+75即可求得面积的最值.
解答 解:设垂直于墙的材料长为x米,
则平行于墙的材料长为27+3-3x=30-3x,
则总面积S=x(30-3x)=-3x2+30x=-3(x-5)2+75,
故饲养室的最大面积为75平方米,
故选A.
点评 本题考查了二次函数的应用,解题的关键是从实际问题中抽象出函数模型,难度不大.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 数轴上表示4的点与表示6的点之间的距离是10 | |
| B. | 数轴上表示-6的点与表示-4的点之间的距离为-10 | |
| C. | 数轴上表示-6的点与表示4的点之间的距离是10 | |
| D. | 数轴上表示-6的点与原点之间的距离是-6 |
5.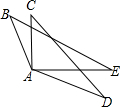 如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
 如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )| A. | ∠B=∠C | B. | ∠D=∠E | C. | ∠BAC=∠EAD | D. | ∠B=∠E |
 如图,在△ABC中,∠A=30°,若∠B=∠C,则∠B的度数是75度.
如图,在△ABC中,∠A=30°,若∠B=∠C,则∠B的度数是75度. 如图,图中共有6条线段,5条射线,0条直线.
如图,图中共有6条线段,5条射线,0条直线.