题目内容
设a=15，b=-3，试确定a2009+b2010的末位数字是几？
解：∵a=15
∴a2009=152009的末位数字一定是5
∵b=-3
∴b2010=（-3）2010=32010
∵31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561，
∴推算32010的末位数字一定是9
∴a2009与b2010的末位数字之和是14
∴a2009+b2010的末位数字是4．
分析：由a=15则a2009=152009的末位数字一定是5，则b2010=（-3）2010=32010，推算32010的末位数字一定是9，而解得．
点评：一个整数的正整数次幂的个位数字有规律，观察a2009=152009的末位数字一定是5的特点，推算32010的末位数字一定是9是解本题的关键．
∴a2009=152009的末位数字一定是5
∵b=-3
∴b2010=（-3）2010=32010
∵31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561，
∴推算32010的末位数字一定是9
∴a2009与b2010的末位数字之和是14
∴a2009+b2010的末位数字是4．
分析：由a=15则a2009=152009的末位数字一定是5，则b2010=（-3）2010=32010，推算32010的末位数字一定是9，而解得．
点评：一个整数的正整数次幂的个位数字有规律，观察a2009=152009的末位数字一定是5的特点，推算32010的末位数字一定是9是解本题的关键．
练习册系列答案
相关题目
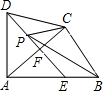如图四边形ABCD中，AD=DC．∠DAB=∠ACB=90°，过点D作DF⊥AC，垂足为F．DF与AB相交于E．设AB=15，BC=9，P是射线DF上的动点．当△BCP的周长最小时，DP的长为（ ）| A、12 | B、12.5 | C、13 | D、13.5 |
设a=
，则实数a在数轴上对应的点的大致位置是（ ）
| 15 |
A、 |
B、 |
C、 |
D、 |
某地销售8 000万元即开型福利彩票（每张面额2元），设特等奖15名，每名奖金100万元，某人花10元买了5张彩票，下列说法中正确的是（ ）
| A、中特等奖是必然事件 | ||
| B、中特等奖是不可能事件 | ||
| C、中特等奖是可能事件，但可能性很小 | ||
D、因为5÷15=
|