题目内容
13.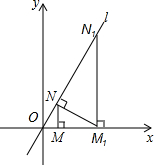 如图,已知直线l:y=$\sqrt{3}$x,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于点N1,过点N1作直线l的垂线交x轴于点M2;…按此作法继续下去,则点M2015的坐标为(42015,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于点N1,过点N1作直线l的垂线交x轴于点M2;…按此作法继续下去,则点M2015的坐标为(42015,0).
分析 本题需先求出OM1和OM2的长,再根据题意得出OMn=4n,求出OM4的长等于44,即可求出M2015的坐标.
解答 解:∵直线l的解析式是y=$\sqrt{3}$x,
∴∠NOM=60°,∠ONM=30°.
∵点M的坐标是(1,0),NM∥y轴,点N在直线y=$\sqrt{3}$x上,
∴NM=$\sqrt{3}$,
∴ON=2OM=2.
又∵NM1⊥l,即∠ONM1=90°
∴OM1=2ON=41OM=4.
同理,OM2=4OM1=42OM,
OM3=4OM2=4×42OM=43OM,
…
OM2015=42015OM,
∴点M2015的坐标是(42015,0).
故答案是:(42015,0).
点评 本题主要考查一次函数图象上点的坐标特点,涉及到如何根据一次的解析式和点的坐标求线段的长度,以及如何根据线段的长度求出点的坐标,解题时要注意相关知识的综合应用.

练习册系列答案
相关题目
8.长方形的周长是36厘米.长是宽的2倍.设长为x厘米,则下列方程正确的是( )
| A. | x+2x=36 | B. | x+$\frac{1}{2}$x=36 | C. | 2(x+2x)=36 | D. | 2(x+$\frac{1}{2}$x)=36 |
18.下列各式不能用平方差公式的是( )
| A. | (x+y)(x-y) | B. | (x+2y)(2x-y) | C. | (x3+y3)(x3-y3) | D. | (-x-y)(x-y) |
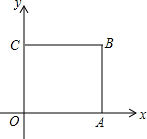 如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.