Question

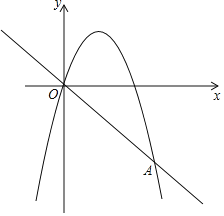
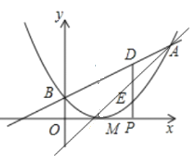
【题目】已知二次函数图象的顶点坐标为，直线与二次函数的图象交于，两点，其中点的坐标为，点在轴上．

（1）求的值及这个二次函数的解析式；

（2）在轴上找一点，使的周长最小，并求出此时点坐标；

（3）若是轴上的一个动点，过作轴的垂线分别于直线和二次函数的图象交于，两点．当时，求线段的最大值；

Answer 1

【答案】（1），；（2）；（3）时，最大长度

【解析】

（1）将点A的坐标代入一次函数的解析式即可求出m的值，根据题意设出二次函数的顶点式，再将点A的坐标代入二次函数的解析式，即可得出二次函数的解析式；

（2）联立一次函数和二次函数的解析式求出点B的坐标，作点B关于x轴的对应点，连接，求出直线的解析式，再令y=0，即可得出答案；

（3）根据P的坐标设出点D和点E的坐标，用点D的纵坐标减去点E的纵坐标即可得出DE的函数解析式，再化为顶点式，即可得出答案.

解：（1）∵过点A(3,4)

∴3+m=4

解得：m=1

又二次函数的顶点M的坐标为(1,0)

∴可设二次函数的解析式为：

又二次函数过点A(3,4)

∴

解得：a=1

∴二次函数的解析式为：

（2）根据题意可得：

解得：或

∴点B的坐标为(0,1)

做点B关于x轴的对称点

连接与x轴的交点即为所求

设直线的解析式为：y=kx+b

∴，解得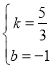

∴直线的解析式为：

当y=0时，x=

故点Q的坐标为()

（3）根据题意可得点D的坐标为，点E的坐标为

当0<a<3时，

∴当a=时，DE最长，此时DE=