Question

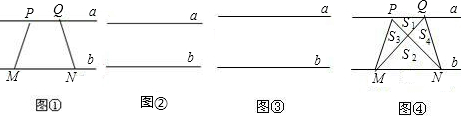
为了探究n条直线能把平面最多分成几部分，我们从最简单的情形入手．
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成11部分…；
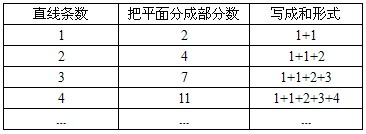
把上述探究的结果进行整理，列表分析：

直线条数	把平面分成部分数	写成和形式
1	2	1+1
2	4	1+1+2
3	7	1+1+2+3
4	11	1+1+2+3+4
…	…	…

（1）当直线条数为5时，把平面最多分成

 

部分，写成和的形式

 

；
（2）当直线为10条时，把平面最多分成

 

部分；
（3）当直线为n条时，把平面最多分成

 

部分．（不必说明理由）

Answer 1

分析：根据表中数据，总结出规律，再根据规律解题．

解答：解：（1）根据表中规律，当直线条数为5时，把平面最多分成16部分，1+1+2+3+4+5=16；
（2）根据表中规律，当直线为10条时，把平面最多分成56部分，为1+1+2+3+…+10=56；
（3）设直线条数有n条，分成的平面最多有m个．
有以下规律：
n             m
1             1+1
2             1+1+2
3             1+1+2+3
：
：
：
n             m=1+1+2+3+…+n=

n(n+1)

2

+1．

点评：本题体现了由“特殊到一般再到特殊”的思维过程，有利于培养同学们的探究意识．