题目内容
1.直线y=x+1与y=-x+7分别与x轴交于A、B两点,两直线相交于点C,则△ABC的面积为12.分析 让两直线组成方程组可得交点C的坐标,让两直线的y=0,可得B,A的坐标,进而求得AB的长度,那么可得△ABC的面积=$\frac{1}{2}$×AB×点C的纵坐标的绝对值.
解答 解:$\left\{\begin{array}{l}{y=x+1}\\{y=-x+7}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,
所以点C的纵坐标为3,
∵y=x+1与x轴的交点为(-1,0),y=-x+7与x轴的交点为(7,0),
∴AB=7-(-1)=8,
∴△ABC的面积=$\frac{1}{2}$×8×3=12.
故答案为:12
点评 考查三角形面积的计算;用到的知识点为:两直线的交点坐标为两直线解析式组成方程组的解.

练习册系列答案
相关题目
13.3-$\sqrt{5}$的绝对值是( )
| A. | 3-$\sqrt{5}$ | B. | $\sqrt{5}$-3 | C. | -3-$\sqrt{5}$ | D. | 3+$\sqrt{5}$ |
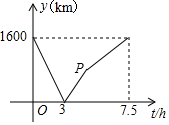 【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示.
【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示. 如图,已知?ABCD.
如图,已知?ABCD.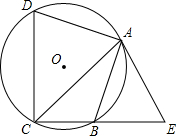 如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.




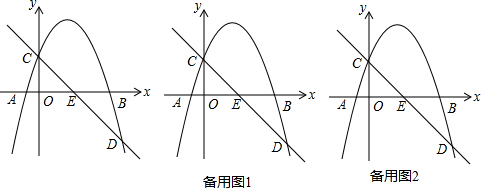
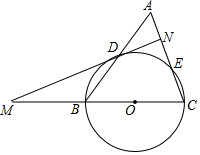 如图,△ABC中,AC=BC=a,AB=b,以BC为直径作⊙O交AB于点D,交AC于点E,过点D作⊙O的切线MN,交CB的延长线于点M,交AC于点N.
如图,△ABC中,AC=BC=a,AB=b,以BC为直径作⊙O交AB于点D,交AC于点E,过点D作⊙O的切线MN,交CB的延长线于点M,交AC于点N.