题目内容
EF是△ABC的中位线,沿EF剪切后,用得到的△AEF和四边形EFCB可以拼成一个平行四边形EDCB.
仿上式的方法,按以下要求完成操作设计,并在规定的位置画出图形
(1)在△ABC中,增加条件________,沿着________只剪切一刀,可以拼成一个矩形.
(2)在△ABC中,增加条件________,沿着________只剪切一刀,可以拼成一个菱形.
(3)在△ABC中,增加条件________,沿着________只剪切一刀,可以拼成一个正方形.
(4)在△ABC中(AB≠AC),只剪切一刀后也可以拼成一个等腰梯形,剪切线的作法是________,然 后沿着剪切线只剪切一刀后,可以拼成一个等腰梯形.
后沿着剪切线只剪切一刀后,可以拼成一个等腰梯形.
解:(1)∠B=90°,中位线EF,或AB=AC高AD;

(2)AB=2BC,中位线EF,或∠C=90°∠A=30°中位线EF;

(3)∠B=90°且AB=2BC,中位线EF,或AB=AC,且∠BAC=90°,中线AD;

(4)法一:设∠B>∠C,在BC上取点D,作∠1=∠B,取AC中点E,过E作EF∥DG交BC于F,则EF为剪切线,
法二:设∠B>∠C,分别取AB、AC中点G、E,过G、E作BC的垂线,垂足为D、H,在HC上截取HF=BD,连EF,则EF为剪切线.

故答案为:(1)∠B=90°,中位线EF;
(2)AB=2BC,中位线EF;
(3)∠B=90°且AB=2BC,中位线EF;
(4)设∠B>∠C,在BC上取点D,作∠1=∠B,取AC中点E,过E作EF∥DG交BC于F,则EF为剪切线.
分析:(1)易知∠B是拼合成的四边形的一个角,任意三角形可拼成平行四边形,而有一个角是90°的平行四边形是矩形,添加∠B=90°沿中位线剪切;
(2)沿中位线裁剪即为平行四边形.BC是拼成四边形的一条边,BC=BE,那么AB=2BC;
(3)易知BE和BC是拼合成的四边形的一组邻边,要是正方形,那么邻边应相等,那么除了添加∠B=90°保证是矩形外,还要添加原三角形的AB边=2BC.
(4)易知过梯形一腰中点与两底相交的线段,把梯形分为两个全等三角形,应先作出AC中点E.把已知三角形先做BC的平行线,得到上底的一部分,做∠EFB=∠B即可.
点评:本题综合考查了三角形的中位线定理,菱形、矩形、正方形及等腰梯形的判定与性质.解答此题时,用到的知识点为:有一个角是直角的平行四边形是矩形;有一组邻边相等的矩形是正方形,同一底上两个角相等的梯形是等腰梯形等.

(2)AB=2BC,中位线EF,或∠C=90°∠A=30°中位线EF;

(3)∠B=90°且AB=2BC,中位线EF,或AB=AC,且∠BAC=90°,中线AD;

(4)法一:设∠B>∠C,在BC上取点D,作∠1=∠B,取AC中点E,过E作EF∥DG交BC于F,则EF为剪切线,
法二:设∠B>∠C,分别取AB、AC中点G、E,过G、E作BC的垂线,垂足为D、H,在HC上截取HF=BD,连EF,则EF为剪切线.

故答案为:(1)∠B=90°,中位线EF;
(2)AB=2BC,中位线EF;
(3)∠B=90°且AB=2BC,中位线EF;
(4)设∠B>∠C,在BC上取点D,作∠1=∠B,取AC中点E,过E作EF∥DG交BC于F,则EF为剪切线.
分析:(1)易知∠B是拼合成的四边形的一个角,任意三角形可拼成平行四边形,而有一个角是90°的平行四边形是矩形,添加∠B=90°沿中位线剪切;
(2)沿中位线裁剪即为平行四边形.BC是拼成四边形的一条边,BC=BE,那么AB=2BC;
(3)易知BE和BC是拼合成的四边形的一组邻边,要是正方形,那么邻边应相等,那么除了添加∠B=90°保证是矩形外,还要添加原三角形的AB边=2BC.
(4)易知过梯形一腰中点与两底相交的线段,把梯形分为两个全等三角形,应先作出AC中点E.把已知三角形先做BC的平行线,得到上底的一部分,做∠EFB=∠B即可.
点评:本题综合考查了三角形的中位线定理,菱形、矩形、正方形及等腰梯形的判定与性质.解答此题时,用到的知识点为:有一个角是直角的平行四边形是矩形;有一组邻边相等的矩形是正方形,同一底上两个角相等的梯形是等腰梯形等.

练习册系列答案
相关题目
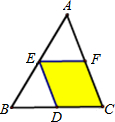 16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为
16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为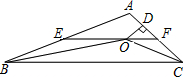 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论: 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论: 17、如图,在ABC中,EF是ABC的中位线,D是BC上任一点(不与B,C重合),AD与EF交于点O,连接DE,DF,要使四边形AEDF是平行四边形,需要添加的条件是
17、如图,在ABC中,EF是ABC的中位线,D是BC上任一点(不与B,C重合),AD与EF交于点O,连接DE,DF,要使四边形AEDF是平行四边形,需要添加的条件是 (2011•宝安区一模)如图,已知AD是△ABC的高,EF是△ABC的中位线,则下列结论中错误的是( )
(2011•宝安区一模)如图,已知AD是△ABC的高,EF是△ABC的中位线,则下列结论中错误的是( )