题目内容
5.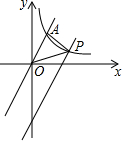 如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,则k=2;△POA的面积为2.
如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,则k=2;△POA的面积为2.
分析 根据直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),可以求得m的值和k的值,从而可以求得反比例函数的解析式,由直线y=2x向下平移4个单位可以得到平移后的函数解析式,从而可以求得点P的坐标,进而求得OP的函数解析式,然后根据点A的坐标,从而可以得到△POA的面积.
解答 解:∵y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),
∴2=2x,得x=1,
∴m=1,
∴2=$\frac{k}{1}$,得k=2,
直线y=2x向下平移4个单位后的函数解析式为y=2x-4,
$\left\{\begin{array}{l}{y=2x-4}\\{y=\frac{2}{x}}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\sqrt{2}+1}\\{y=2\sqrt{2}-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{2}+1}\\{y=-2\sqrt{2}-2}\end{array}\right.$(舍去),
∴点P的坐标为($\sqrt{2}+1$,$2\sqrt{2}-2$),
设OP对应的函数解析式为y=ax,
$2\sqrt{2}-2=a×(\sqrt{2}+1)$,
得a=6-4$\sqrt{2}$,
∴OP对应的函数解析式为y=(6-4$\sqrt{2}$)x,
当x=1时,y=(6-4$\sqrt{2}$)×1=6-4$\sqrt{2}$,
∴△POA的面积是:$\frac{2-(6-4\sqrt{2})}{2}×(\sqrt{2}+1)$=2,
故答案为:2,2.
点评 本题考查反比例函数与一次函数的交点问题、一次函数图象与几何变化,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | $\sqrt{21}$ | B. | $\sqrt{35}$ | C. | $\sqrt{42}$ | D. | $\root{3}{64}$ |
| A. | 要了解某大洋的海水污染质量情况,宜采用全面调查方式 | |
| B. | 如果有一组数据为5,3,6,4,2,那么它的中位数是6 | |
| C. | 为了解怀化市6月15日到19日的气温变化情况,应制作折线统计图 | |
| D. | “打开电视,正在播放怀化新闻节目”是必然事件 |

 如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为64°.
如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为64°.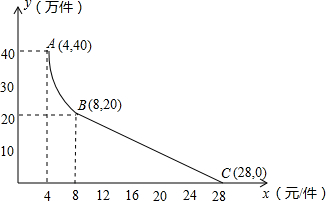 月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
 如图,已知边长为1的小正方形组成的网格中有一个△ABC,点A、B、C均在格点上.
如图,已知边长为1的小正方形组成的网格中有一个△ABC,点A、B、C均在格点上.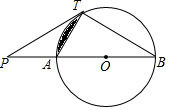 如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.