题目内容
12.如图,在平面直角坐标系中,定线段AB长为4,它的两端点A、B分别落在y轴正半轴和x轴正半轴上,P为AB的中点.(1)若A(0,2$\sqrt{3}$),求∠ABO的度数;
(2)将(1)中的A点向下平移m个单位到达A′处,此时,B点随之沿x轴向右移动到B′处,此时线段A′B′的中点为P′.
①若m=$\sqrt{3}$时,求B′点和P′点的坐标;
②m为何值时,∠POP′=15°?请直接写出此时AB的中点P运动的路径长.
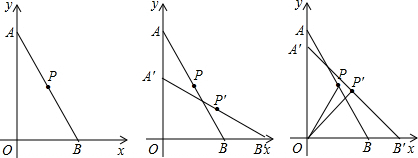
分析 (1)通过解直角三角形和特殊角的三角函数值进行解答;
(2)①在直角△A′OB′中利用勾股定理可以求得点B′的坐标;结合中点坐标公式来求P′点的坐标;
②△APO和△P′A′O都是等腰三角形,根据等腰三角形的两底角相等,即可求得∠PAO的度数和∠P′A′O的度数,在直角△ABO和△A′B′O中,根据三角函数即可求得OA与OA′,即可求得AA′的长.中点P的运动路径是以点O为圆心,圆心角为15°,半径长为OP的弧长.
解答  解:(1)如图1,∵A(0,2$\sqrt{3}$),
解:(1)如图1,∵A(0,2$\sqrt{3}$),
∴OA=2$\sqrt{3}$,AB=4,
∴sin∠ABO=$\frac{OA}{AB}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠ABO=60°;
(2)①如图2,∵m=$\sqrt{3}$,A(0,2$\sqrt{3}$),
∴A′(0,$\sqrt{3}$),
∴OA′=$\sqrt{3}$,
又∵在直角△A′OB′中,A′B′=4,
∴OB′=$\sqrt{A′B{′}^{2}-OA{′}^{2}}$=$\sqrt{{4}^{2}-(\sqrt{3})^{2}}$=$\sqrt{13}$,
则点B′的坐标是($\sqrt{13}$,0).
又∵线段A′B′的中点为P′,
∴点P′的坐标为:($\frac{\sqrt{13}}{2}$,$\frac{\sqrt{3}}{2}$);
②∵点P和点P′分别是Rt△AOB的斜边AB与Rt△A′OB′的斜边A′B′的中点,
∴PA=PO,P′A′=P′O,
∴∠PAO=∠AOP,∠P′A′O=∠A′OP′.
∴∠P′A′O-∠PAO=∠POP′=15°.
∵∠PAO=30°,
∴∠P′A′O=45°.
∴A′O=A′B′×cos45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$.
∴AA′=OA-A′O=2$\sqrt{3}$米.
∵AB=4,OP是AB的中点,
∴OP=$\frac{1}{2}$AB=2.
∴AB的中点P运动的路径长为:$\frac{15π×2}{180}$=$\frac{π}{6}$.
点评 本题考查了几何变换综合题.解答(2)②题的妙处在于恰到好处地利用了直角三角形斜边上的中线等于斜边的一半,从而求出∠P′A′O=45°.

| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 85 | 75 |
(1)两所学校报名参加旅游的学生人数之和是多少人?
(2)两所学校报名参加旅游的学生各有多少人?
| A. | 近似数2.4×104精确到十分位 | |
| B. | 将数60340精确到千位是6.0×104 | |
| C. | 按科学记数法表示的6.05×105,其原数是60500 | |
| D. | 近似数8.1750是精确到0.001 |
 如图,在△ABC中,DE∥BC,EF∥CD,求证:$\frac{AF}{AD}=\frac{AD}{AB}$.
如图,在△ABC中,DE∥BC,EF∥CD,求证:$\frac{AF}{AD}=\frac{AD}{AB}$.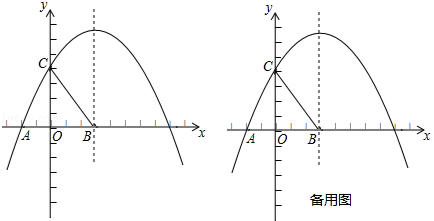
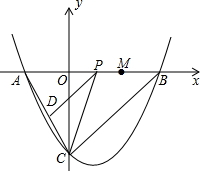 已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).
已知:如图,抛物线y=a(x-1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(-2,0).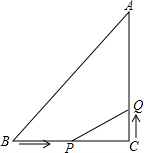 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.