题目内容
18.在同一条道路上,甲行走的速度为3km/h,出发后0.15h后,乙以4.5km/h的速度追甲.设乙行走的时间为t(h).(1)写出甲、乙两人所走的路程s与时间t的函数表达式.
(2)在同一直角坐标系中画出它们的图象.
(3)求出两条直线的交点坐标,并说明它的实际意义.
分析 (1)根据速度乘以时间等于路程,可得函数解析式;
(2)根据一次函数的图象是一条直线,而两点确定一条直线,结合自变量的取值范围可得函数图象;
(3)根据函数图象解答即可.
解答  解:(1)由题意得:
解:(1)由题意得:
S甲=3t+0,45,
S乙=4.5t;
(2)它们的图象如图所示:
(3)由图象可知:
两条直线的交点坐标为(0.3,1.35),
表示的实际意义是:乙出发0.3小时后追上甲.
点评 本题考查了一次函数的应用,读懂题目信息,得出甲、乙两同学每人所走的路程s与时间t的关系是解题的关键.

练习册系列答案
相关题目
6.某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
甲、乙两所学校计划组织本校学生自愿参加此项活动,已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20800元,若两校联合组团只需花费18000元.
(1)两所学校报名参加旅游的学生人数之和是多少人?
(2)两所学校报名参加旅游的学生各有多少人?
| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 85 | 75 |
(1)两所学校报名参加旅游的学生人数之和是多少人?
(2)两所学校报名参加旅游的学生各有多少人?
5.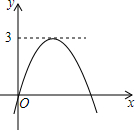 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最小值为( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最小值为( )
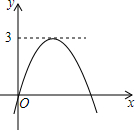 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最小值为( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最小值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 9 |
 如图,在△ABC中,DE∥BC,EF∥CD,求证:$\frac{AF}{AD}=\frac{AD}{AB}$.
如图,在△ABC中,DE∥BC,EF∥CD,求证:$\frac{AF}{AD}=\frac{AD}{AB}$.