题目内容
19.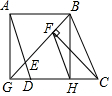 如图,四边形ABHG是正方形,D,C在射线GH上,四边形ABCD是平行四边形,CF⊥BG于F,BG,AD交于点E,连HF.
如图,四边形ABHG是正方形,D,C在射线GH上,四边形ABCD是平行四边形,CF⊥BG于F,BG,AD交于点E,连HF.(1)求证:DG=HC;
(2)求证:AD=$\sqrt{2}$HF;
(3)若EG=2,BF=3,直接写出EF的值.
分析 (1)只要证明GH=CD,即可推出GD=HC;
(2)只要证明△FGH∽△CGB,即可推出$\frac{FH}{BC}$=$\frac{GH}{BG}$=$\frac{1}{\sqrt{2}}$,由此即可解决问题;
(3)如图3中,连接DF,将△AGE绕点A逆时针性质90°得到△ABM.首先证明△ADF是等腰直角三角形,再证明△AFM≌△AFE,推出EF=FM,由∠MBF=90°,可得EF=FM=$\sqrt{B{M}^{2}+B{F}^{2}}$,由此即可解决问题;
解答 (1)证明:如图1中,
∵四边形ABHG是正方形,
∴AB=GH,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴HG=CD,
∴GH-DH=CD-DH,
即DG=HC;
(2)证明:如图2中,
∵∠FGC=∠BGH,∠CFG=∠BHG=90°,
∴△CFG∽△BHG,
∴$\frac{FG}{GH}$=$\frac{GC}{BG}$,
∴$\frac{FG}{GC}$=$\frac{GH}{BG}$,∵∠FGH=∠CGB,
∴△FGH∽△CGB,
∴$\frac{FH}{BC}$=$\frac{GH}{BG}$=$\frac{1}{\sqrt{2}}$,
∴BC=$\sqrt{2}$FH,
∵AD=CB,
∴AD=$\sqrt{2}$FH.
(3)解:如图3中,连接DF,将△AGE绕点A逆时针性质90°得到△ABM.
∵CF⊥BG,∠FGC=45°,
∴FG=FC,∠FGD=∠FCH=45°,∵GD=HC,
∴△FGD≌△FCH,
∴FD=FH,
易证△FGA≌△GFH,
∴AF=FH=FD,
∵AD=$\sqrt{2}$FH,
∴AD=$\sqrt{2}$AF=$\sqrt{2}$DF,
∴△DAF是等腰直角三角形,
∴∠FAE=45°,
∴∠MAF=∠MAB+∠BAF=∠GAE+∠BAF=45°=∠FAE,
∵AF=AF,AM=AE,
∴△AFM≌△AFE,
∴EF=FM,
∵∠ABM=∠AGE=45°,
∴∠MBF=90°,
∴EF=FM=$\sqrt{B{M}^{2}+B{F}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、平行四边形的判定和性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题、学会添加常用辅助线构造全等三角形解决问题,属于中考压轴题.

| A. | 0 | B. | $\frac{1}{2}$ | C. | 0或$\frac{1}{2}$ | D. | 1或 2 |
| A. | 3.6 | B. | 3.8 | C. | 3.6或3.8 | D. | 4.2 |
 如图是二次函数y=a(x+1)2+2图象的一部分,则关于x的不等式a(x+1)2+2>0的解集是( )
如图是二次函数y=a(x+1)2+2图象的一部分,则关于x的不等式a(x+1)2+2>0的解集是( )| A. | x<2 | B. | x>-3 | C. | -3<x<1 | D. | x<-3或x>1 |
| 华为手机 | 苹果手机 | |
| 进价(元/部) | 2000 | 4400 |
| 售价(元/部) | 2500 | 5000 |
(1)苹果手机至少购进多少部?
(2)该商场应该怎样进货,使全国销售后获得的毛利润最大?并求出最大毛利润.
 如图,AB∥CD,已知∠BED=64°,BC平分∠ABE,则∠ABC的度数是( )
如图,AB∥CD,已知∠BED=64°,BC平分∠ABE,则∠ABC的度数是( )| A. | 16° | B. | 32° | C. | 64° | D. | 116° |
| A. | 8,6 | B. | 6,8 | C. | 6,6 | D. | 8,10 |
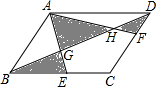 如图,在平行四边形ABCD中,BE=EC,CF=2FD.求阴影面积和空白面积的比?
如图,在平行四边形ABCD中,BE=EC,CF=2FD.求阴影面积和空白面积的比?