题目内容
 如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.(1)已知两条抛物线①:y=x2+2x-1,②:y=-x2+2x+1,判断这两条抛物线是否关联,并说明理由.
(2)抛物线C1:y=
| 1 |
| 8 |
(3)若A为抛物线C1:y=
| 1 |
| 8 |
考点:二次函数综合题
专题:
分析:(1)首先求得抛物线①的顶点坐标,然后检验是否此点在抛物线②与③上,再求得抛物线②的顶点坐标,检验是否在抛物线①上即可求得答案;
(2)首先求得抛物线C1的顶点坐标,则可得:点P在直线y=2上,则可作辅助线:作M关于P的对称点N,分别过点M、N作直线y=2的垂线,垂足为E,F,则可求得:点N的坐标,利用顶点式即可求得结果;
(3)根据全等三角形的知识,即可求得点B的坐标,从而求得B′点的坐标.
(2)首先求得抛物线C1的顶点坐标,则可得:点P在直线y=2上,则可作辅助线:作M关于P的对称点N,分别过点M、N作直线y=2的垂线,垂足为E,F,则可求得:点N的坐标,利用顶点式即可求得结果;
(3)根据全等三角形的知识,即可求得点B的坐标,从而求得B′点的坐标.
解答:解:(1)∵①抛物线y=x2+2x-1=(x+1)2-2的顶点坐标为M(-1,-2),
∴②当x=-1时,y=-x2+2x+1=-1-2+1=-2,
∴点M在抛物线②上;
∴抛物线①与抛物线②有关联;
∵抛物线②y=-x2+2x+1=-(x-1)2+2,其顶点坐标为(1,2),
经验算:(1,2)在抛物线①上,
∴抛物线①、②是关联的;

(2)抛物线C1:y=
(x+1)2-2的顶点M的坐标为(-1,-2),
∵动点P的坐标为(t,2),
∴点P在直线y=2上,
作M关于P的对称点N,分别过点M、N作直线y=2的垂线,垂足为E,F,则ME=NF=4,
∴点N的纵坐标为6,
当y=6时,
(x+1)2-2=6,
解得:x1=7,x2=-9,
①设抛物C2的解析式为:y=a(x-7)2+6,
∵点M(-1,-2)在抛物线C2上,
∴-2=a(-1-7)2+6,
∴a=-
.
∴抛物线C2的解析式为:y=-
(x-7)2+6;
②设抛物C2的解析式为:y=a(x+9)2+6,
∵点M(-1,-2)在抛物线C2上,
∴-2=a(-1+9)2+6,
∴a=-
.
∴抛物线C2的解析式为:y=-
(x+9)2+6;

(3)若A为抛物线C1:y=
(x+1)2-2的顶点,
∴A(-1,-2),
∵点B′恰好在y轴上,
∴AN=1,
∵BA⊥B′A,
∴∠BAM+∠B′AN=90°,
∵∠BAM+∠ABM=90°,
∴∠ABM=∠B′AN,
∵AB=AB′,
∴△ABM≌△B′AN,
∴BM=AN=1,AM=B′N,
∴B点的纵坐标为-1,
把y=-1代入y=
(x+1)2-2
解得:x=-1+2
或x=-1-2
,
∴B′(0,2
-2)或(0,-2-2
),
∴点B′的纵坐标是(0,2
-2)或(0,-2-2
).
∴②当x=-1时,y=-x2+2x+1=-1-2+1=-2,
∴点M在抛物线②上;
∴抛物线①与抛物线②有关联;
∵抛物线②y=-x2+2x+1=-(x-1)2+2,其顶点坐标为(1,2),
经验算:(1,2)在抛物线①上,
∴抛物线①、②是关联的;

(2)抛物线C1:y=
| 1 |
| 8 |
∵动点P的坐标为(t,2),
∴点P在直线y=2上,
作M关于P的对称点N,分别过点M、N作直线y=2的垂线,垂足为E,F,则ME=NF=4,
∴点N的纵坐标为6,
当y=6时,
| 1 |
| 8 |
解得:x1=7,x2=-9,
①设抛物C2的解析式为:y=a(x-7)2+6,
∵点M(-1,-2)在抛物线C2上,
∴-2=a(-1-7)2+6,
∴a=-
| 1 |
| 8 |
∴抛物线C2的解析式为:y=-
| 1 |
| 8 |
②设抛物C2的解析式为:y=a(x+9)2+6,
∵点M(-1,-2)在抛物线C2上,
∴-2=a(-1+9)2+6,
∴a=-
| 1 |
| 8 |
∴抛物线C2的解析式为:y=-
| 1 |
| 8 |

(3)若A为抛物线C1:y=
| 1 |
| 8 |
∴A(-1,-2),
∵点B′恰好在y轴上,
∴AN=1,
∵BA⊥B′A,
∴∠BAM+∠B′AN=90°,
∵∠BAM+∠ABM=90°,
∴∠ABM=∠B′AN,
∵AB=AB′,
∴△ABM≌△B′AN,
∴BM=AN=1,AM=B′N,
∴B点的纵坐标为-1,
把y=-1代入y=
| 1 |
| 8 |
解得:x=-1+2
| 2 |
| 2 |
∴B′(0,2
| 2 |
| 2 |
∴点B′的纵坐标是(0,2
| 2 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式以及二次函数的顶点坐标的求解方法,全等三角形的性质等知识.此题综合性很强,难度较大,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
 如图,CD平分∠ACB,DE∥AC,若∠1=76°,则∠EDC=
如图,CD平分∠ACB,DE∥AC,若∠1=76°,则∠EDC=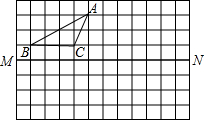 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.请在图中方格纸中,按要求完成下列各题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.请在图中方格纸中,按要求完成下列各题: 如图,直线y1=
如图,直线y1= 如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100km..问:A市与C、D两市分别相距多少千米?(结果精确到1km)
如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100km..问:A市与C、D两市分别相距多少千米?(结果精确到1km)