题目内容
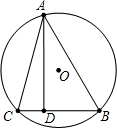 如图,在⊙O的内接△ABC中,AD⊥BC于D点,∠CAB=45°,BD=3,CD=2,则AD=________.
如图,在⊙O的内接△ABC中,AD⊥BC于D点,∠CAB=45°,BD=3,CD=2,则AD=________.
6
分析:设AD=x,则由勾股定理求出AC=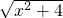 ,AB=
,AB= ,根据S△ABC=
,根据S△ABC= AC×ABsin∠CAB,推出S△ABC=
AC×ABsin∠CAB,推出S△ABC=
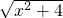 •
• •
• ,根据三角形的面积公式得出S△ABC=
,根据三角形的面积公式得出S△ABC= BC×AD=
BC×AD= ,推出
,推出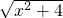 •
• •
• =5x,求出方程的解即可.
=5x,求出方程的解即可.
解答:设AD=x,则由勾股定理得:AC=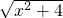 ,AB=
,AB= ,
,
∴S△ABC= AC×ABsin∠CAB,
AC×ABsin∠CAB,
∴S△ABC=
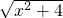 •
• •
• ,
,
∵S△ABC= BC×AD=
BC×AD= ,
,
∴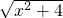 •
• •
• =5x,
=5x,
∴x=±1,x=±6,
∵x表示高AD长,
∴x=±1,x=-6舍去,
∴AD=x=6,
故答案为:6.
点评:本题考查了圆内接四边形和三角形的面积的应用,主要考查学生运用性质进行计算的能力,题目比较典型,但有一定的难度.
分析:设AD=x,则由勾股定理求出AC=
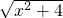 ,AB=
,AB= ,根据S△ABC=
,根据S△ABC= AC×ABsin∠CAB,推出S△ABC=
AC×ABsin∠CAB,推出S△ABC=
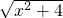 •
• •
• ,根据三角形的面积公式得出S△ABC=
,根据三角形的面积公式得出S△ABC= BC×AD=
BC×AD= ,推出
,推出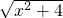 •
• •
• =5x,求出方程的解即可.
=5x,求出方程的解即可.解答:设AD=x,则由勾股定理得:AC=
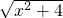 ,AB=
,AB= ,
,∴S△ABC=
 AC×ABsin∠CAB,
AC×ABsin∠CAB,∴S△ABC=

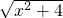 •
• •
• ,
,∵S△ABC=
 BC×AD=
BC×AD= ,
,∴
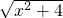 •
• •
• =5x,
=5x,∴x=±1,x=±6,
∵x表示高AD长,
∴x=±1,x=-6舍去,
∴AD=x=6,
故答案为:6.
点评:本题考查了圆内接四边形和三角形的面积的应用,主要考查学生运用性质进行计算的能力,题目比较典型,但有一定的难度.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
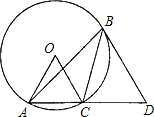 如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )
如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )A、1+
| ||||
B、
| ||||
C、
| ||||
D、
|
 7、已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )
7、已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )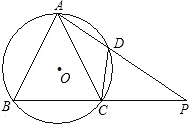 如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.
如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.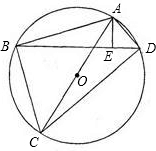 如图,在⊙O的内接四边形ABCD中,AB+AD=12,对角线AC是⊙O的直径,AE⊥BD,垂足为E,AE=3.设⊙O的半径为y,AB的长为x.
如图,在⊙O的内接四边形ABCD中,AB+AD=12,对角线AC是⊙O的直径,AE⊥BD,垂足为E,AE=3.设⊙O的半径为y,AB的长为x. 如图,在⊙O的内接四边形ABCD中,∠BOD=90°,则∠A=
如图,在⊙O的内接四边形ABCD中,∠BOD=90°,则∠A=