题目内容
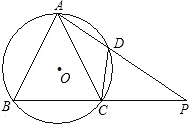 如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.
如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.(1)求证:AB2=AD•AP;
(2)若⊙O的直径为25,AB=20,AD=15,求PC和DC的长.
分析:(1)欲证AB2=AD•AP,需证AC2=AD•AP,因此只需证△ADC∽△ACP即可;
(2)由(1)的结论可求出AP的长,过点A作直径AE交BC于点F,用相交弦定理的推论可求出AF的长,进而可求出BF、CF的长.在Rt△APF中,已知AP、AF的长,可用勾股定理求出PF的长,进而可求出PC的长,根据割线定理,可求出PD的长.
(2)由(1)的结论可求出AP的长,过点A作直径AE交BC于点F,用相交弦定理的推论可求出AF的长,进而可求出BF、CF的长.在Rt△APF中,已知AP、AF的长,可用勾股定理求出PF的长,进而可求出PC的长,根据割线定理,可求出PD的长.
解答:(1)证明:∵∠ADC+∠B=180°,∠B=∠ACB
∴∠ACP+∠ACB=∠ACP+∠B=180°
∴∠ADC=∠ACP
∴△ADC∽△ACP
∴
=
,即
=
所以AB2=AD•AP;
(2)解:过点A作直径AE交BC于点F.
∵△ABC是等腰三角形,
∴AE垂直平分BC
设AF=a,则EF=25-a,BF=
由BF2=AF•EF,得400-a2=a(25-a)
所以AF=a=16,BF=FC=12.
方法1:
由(1)AB2=AD•AP得:AP=
=
=
在Rt△AFP中,PF=
=
=
∴PC=PF-FC=
-12=
又由△PCD∽△PAB得:
=
∴DC=
=
=7;
方法2:(前面部分给分相同)连接BE、EC、BD.
∵AE是直径,
∴∠ABE=90°,且BE=
=15
∴EC=BE=15,又已知AD=15,∴AD=EC
∴DC∥AE,即DC⊥BC,则BD是直径
∴DC=
=
=7
在Rt△PCD中,PD=PA-AD=
-15=
∴PC=
=
.
∴∠ACP+∠ACB=∠ACP+∠B=180°
∴∠ADC=∠ACP
∴△ADC∽△ACP
∴
| AD |
| AC |
| AC |
| AP |
| AD |
| AB |
| AB |
| AP |
所以AB2=AD•AP;
(2)解:过点A作直径AE交BC于点F.

∵△ABC是等腰三角形,
∴AE垂直平分BC
设AF=a,则EF=25-a,BF=
| 400-a2 |
由BF2=AF•EF,得400-a2=a(25-a)
所以AF=a=16,BF=FC=12.
方法1:
由(1)AB2=AD•AP得:AP=
| AB2 |
| AD |
| 400 |
| 15 |
| 80 |
| 3 |
在Rt△AFP中,PF=
| AP2-AF2 |
(
|
| 64 |
| 3 |
∴PC=PF-FC=
| 64 |
| 3 |
| 28 |
| 3 |
又由△PCD∽△PAB得:
| DC |
| AB |
| PC |
| PA |
∴DC=
| PC•AB |
| PA |
| 28×20 |
| 80 |
方法2:(前面部分给分相同)连接BE、EC、BD.
∵AE是直径,
∴∠ABE=90°,且BE=
| 252-202 |
∴EC=BE=15,又已知AD=15,∴AD=EC
∴DC∥AE,即DC⊥BC,则BD是直径
∴DC=
| BD2-BC2 |
| 252-242 |
在Rt△PCD中,PD=PA-AD=
| 80 |
| 3 |
| 35 |
| 3 |
∴PC=
(
|
| 28 |
| 3 |
点评:本题考查了相似三角形的判定和性质、圆内接四边形的性质、等腰三角形的性质等知识的综合应用.综合性强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
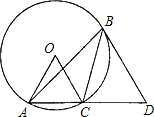 如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )
如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )A、1+
| ||||
B、
| ||||
C、
| ||||
D、
|
 7、已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )
7、已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )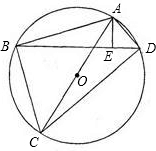 如图,在⊙O的内接四边形ABCD中,AB+AD=12,对角线AC是⊙O的直径,AE⊥BD,垂足为E,AE=3.设⊙O的半径为y,AB的长为x.
如图,在⊙O的内接四边形ABCD中,AB+AD=12,对角线AC是⊙O的直径,AE⊥BD,垂足为E,AE=3.设⊙O的半径为y,AB的长为x. 如图,在⊙O的内接四边形ABCD中,∠BOD=90°,则∠A=
如图,在⊙O的内接四边形ABCD中,∠BOD=90°,则∠A=