题目内容
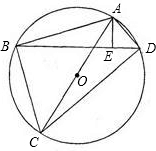 如图,在⊙O的内接四边形ABCD中,AB+AD=12,对角线AC是⊙O的直径,AE⊥BD,垂足为E,AE=3.设⊙O的半径为y,AB的长为x.
如图,在⊙O的内接四边形ABCD中,AB+AD=12,对角线AC是⊙O的直径,AE⊥BD,垂足为E,AE=3.设⊙O的半径为y,AB的长为x.(1)求y与x函数关系式;
(2)当AB的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积.
分析:(1)根据圆周角定理,可知∠ABE=∠ACD,而等角的三角函数值相等,于是可得关于x、y的比例关系式,整理可得函数解析式;
(2)根据(1)中的函数解析式,结合二次函数的性质,可求当x等于多少时,y的最大值,从而求出半径,再利用圆的面积公式可求⊙O的面积.
(2)根据(1)中的函数解析式,结合二次函数的性质,可求当x等于多少时,y的最大值,从而求出半径,再利用圆的面积公式可求⊙O的面积.
解答:解:(1)∵∠ABE=∠ACD,
∴sin∠ABE=sin∠ACD,
∴
=
,
∴y=-
x2+2x.
(2)根据(1)中的函数解析式,
当x=-
=
=6时,
y有最大值,且最大值=
=
=6,
即当x=6时,半径y有最大值是6,
∴S⊙O=πy2=36π.
∴sin∠ABE=sin∠ACD,
∴
| 12-x |
| 2y |
| 3 |
| x |
∴y=-
| 1 |
| 6 |
(2)根据(1)中的函数解析式,
当x=-
| b |
| 2a |
| -2 | ||
2×(-
|
y有最大值,且最大值=
| 4ac-b2 |
| 4a |
4×(-
| ||
4×(-
|
即当x=6时,半径y有最大值是6,
∴S⊙O=πy2=36π.
点评:本题主要考查了圆周角定理、三角函数值、二次函数的性质,此题难度较大.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目

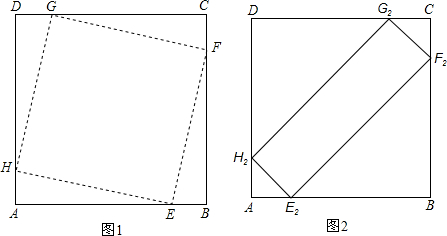
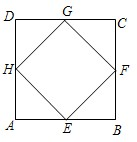 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.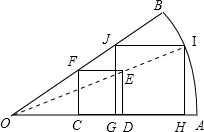
 我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.