题目内容
7.关于x的方程x2+4x+m=0的两根为x1,x2满足|x1-x2|=2,求实数m的值.分析 先根据判别式的意义得到m<4,根据根与系数的关系得到x1+x2=-4,x1x2=m,再把|x1-x2|=2两边平方后利用完全平方公式变形得到(x1+x2)2-4x1x2=4,于是有(-4)2-4m=4,然后解关于m的方程即可得到满足条件的m的值.
解答 解:根据题意得△=42-4m>0,解得m<4,
x1+x2=-4,x1x2=m,
∵|x1-x2|=2,
∴(x1-x2)2=4,
∴(x1+x2)2-4x1x2=4,
即(-4)2-4m=4,
∴m=3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
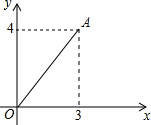 如图,在直角坐标系中,线段OA的两个端点坐标分别为O(0,0),A(3,4),若把线段OA向右平移2个单位,得线段O′A′,则点O′的坐标为(2,0),点A′的坐标为(5,3).
如图,在直角坐标系中,线段OA的两个端点坐标分别为O(0,0),A(3,4),若把线段OA向右平移2个单位,得线段O′A′,则点O′的坐标为(2,0),点A′的坐标为(5,3). 如图,点D是△ABC内一点,连接BD、CD.
如图,点D是△ABC内一点,连接BD、CD.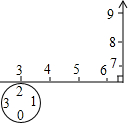 如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2013将与圆周上的数字0重合.
如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2013将与圆周上的数字0重合.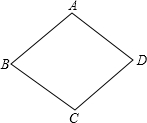 如图,已知菱形ABCD,画一个矩形,使得A,B,C,D四点分别在矩形的四条边上,且矩形的面积为菱形ABCD面积的2倍.
如图,已知菱形ABCD,画一个矩形,使得A,B,C,D四点分别在矩形的四条边上,且矩形的面积为菱形ABCD面积的2倍.