题目内容
已知在平行四边形ABCD中AC,BD交于点O,△AOB的面积为2,那么?ABCD的面积为________.
8
分析:因为平行四边形的对角线互相平分,所以平行四边形被对角线分成的四部分的面积相等,即?ABCD的面积=△AOB的面积×4.
解答:∵四边形ABCD是平行四边形,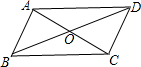
∴OA=OC,OB=OD,AD=BC,AB=CD,
∴△AOB≌△COD,△BOC≌△DOA,
又AO是△ABD的中线,
∴△AOB与△AOD的面积相等,
故?ABCD的面积=△AOB的面积×4=2×4=8,
故答案为:8.
点评:此题主要考查了平行四边形的对角线互相平分的性质.
分析:因为平行四边形的对角线互相平分,所以平行四边形被对角线分成的四部分的面积相等,即?ABCD的面积=△AOB的面积×4.
解答:∵四边形ABCD是平行四边形,

∴OA=OC,OB=OD,AD=BC,AB=CD,
∴△AOB≌△COD,△BOC≌△DOA,
又AO是△ABD的中线,
∴△AOB与△AOD的面积相等,
故?ABCD的面积=△AOB的面积×4=2×4=8,
故答案为:8.
点评:此题主要考查了平行四边形的对角线互相平分的性质.

练习册系列答案
相关题目
已知在平行四边形ABCD中,向量
=
,
=
,那么向量
等于( )
| AB |
| a |
| BC |
| b |
| BD |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
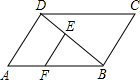 如图,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE:EB=2:3,EF=9,那么BC的长为
如图,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE:EB=2:3,EF=9,那么BC的长为 如图,已知在平行四边形ABCD中,DE:EC=2:3,
如图,已知在平行四边形ABCD中,DE:EC=2:3, 18、已知在平行四边形ABCD中,DE⊥AB,DF⊥BC,∠EDF=135°,求平行四边形各角的度数.
18、已知在平行四边形ABCD中,DE⊥AB,DF⊥BC,∠EDF=135°,求平行四边形各角的度数.