��Ŀ����
��ʢ��˾�мס������������Ŷӣ�ͬʱ����ͬ�ֲ�Ʒ��12���º�ͳ�Ƶó�������Ϣ���������Ŷӵ�x����������y1���������x֮��ĺ�����ϵΪy1=a��x��4��2+
 ���������Ŷӵ�x����������y2���������x֮��ĺ�����ϵΪy2=kx+1��1��x��12��xΪ���������ס������������Ŷ��ڵ�1���µ���������ͬ����Ϊ
���������Ŷӵ�x����������y2���������x֮��ĺ�����ϵΪy2=kx+1��1��x��12��xΪ���������ס������������Ŷ��ڵ�1���µ���������ͬ����Ϊ
 �������
�������
��1���ֱ���y1��y2�ĺ�������ʽ��
��2��̽���м������������Ŷӱȼ������Ŷӵ������ߣ����������߳����������
��3��ֱ��д�����ж��ٸ��¼ס������������Ŷӵ���������������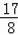
 �����
�����
�����㡿���κ�����Ӧ�ã�
����������1�����ݼס������������Ŷ��ڵ�1���µ���������ͬ����Ϊ
 �������������y1��y2�ⷽ�̼��ɣ�
�������������y1��y2�ⷽ�̼��ɣ�
��2������y2��y1=0�����ö��κ�����һԪ���η����Լ�һԪ���β���ʽ�Ĺ�ϵ������⣻
��3�������ò���ʽ�������⣮
����𡿽⣺��1���ס������������Ŷ��ڵ�1���µ���������ͬ����Ϊ
 ���������
���������
��
 =9a+
=9a+
 ��
��
 =k+1��
=k+1��
��ã�a=
 ��k=
��k=
 ��
��
��y1=
 ��x��4��2+
��x��4��2+
 ��y2=
��y2=
 x+1��
x+1��
��2��y1��y2=
 ��x��4��2+
��x��4��2+
 ��
��
 x+1=��
x+1=��
 ��x��5��2+2��
��x��5��2+2��
��y1��y2=0���ⷽ�̵ã�x1=1��x2=9��
��Ϻ�����ͼ���֪����1��x��9ʱ��y1��y2��0����y1��y2
��xΪ��������x=2��3��4��5��6��7��8������7�����������Ŷӱȼ������Ŷӵ������ߣ���x=5ʱ���������߳�2�����
��3���ס������������Ŷӵ���������������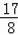
 �����
�����
��
 ��x��4��2+
��x��4��2+
 ��
��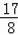
 �٣�
�٣�
 x+1��
x+1��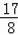
 �ڣ�
�ڣ�
�ɢٵã�0��x��8���ɢڵã�x��4.5
�֡�xΪ������
��x=5��6��7��8����4���¼ס������������Ŷӵ���������������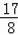
 �����
�����
��������������Ҫ�����˶��κ�����һ�κ����뷽�̺Ͳ���ʽ�Ĺ�ϵ���ܹ��������������ν��˼�룬��Ϻ���ͼ��ⲻ��ʽ�ǽ������Ĺؼ���

 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�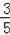
 ������������y=
������������y=


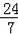
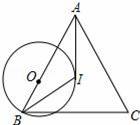


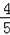
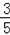
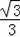

 2��2y2��1
2��2y2��1 ��0 D����a������b��
��0 D����a������b��

 B����
B���� ��ab=1������a﹣2����b﹣2���Ľ����__________��
��ab=1������a﹣2����b﹣2���Ľ����__________��