题目内容
已知直线y=kx﹣7经过点(2,﹣1),求关于x的不等式kx﹣7≥0的解集.
【考点】一次函数与一元一次不等式.
【分析】根据图象经过的点的坐标满足函数解析式,可得关于k的方程,根据解方程,可得k值,根据解不等式,可得答案.
【解答】解:由直线y=kx﹣7经过点(2,﹣1),得
2k﹣7=﹣1,
解得k=3.
kx﹣7≥0即为3x﹣7≥0.
解3x﹣7≥0,解得x≥
 .
.
【点评】本题考查了一次函数与一元一次不等式,先利用图象上的点求出k值,再求出不等式的解集.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A.1 B.2 C.3 D.4
 得的利润恰是销售收入的20%,如果笫一天的销售收入为4万元,且每天的销售收入都有增长.笫三天的利润是0.968万元.
得的利润恰是销售收入的20%,如果笫一天的销售收入为4万元,且每天的销售收入都有增长.笫三天的利润是0.968万元.

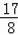
 万件.
万件.
 =1
=1