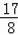题目内容
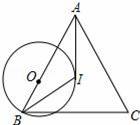
如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=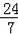
 ,则sin∠C的值为( )
,则sin∠C的值为( )

A.
 B.
B.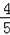
 C.
C.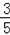
 D.
D.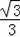

B【考点】三角形的内切圆与内心.
【专题】计算题.
【分析】延长AI交BC于D,连结OI,作BH⊥AC于H,如图,根据内心的性质得∠OBI=∠DBI,则可证明OI∥BD,再根据切线的性质得OI⊥AI,则BD⊥AD,加上AI平分∠BAC,所以△ABC为等腰三角形,得到AB=AC,接着在Rt△ABH中,利用正切的定义得到tan∠BAH=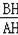
 =
=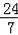
 ,于是可设BH=24x,AH=7x,利用勾股定理得到AB=25x,则AC=AB=25x,CH=AC﹣AH=18x,然后在Rt△BCH中,利用勾股定理计算出BC=30x,再利用正弦的定义计算sinC的值.
,于是可设BH=24x,AH=7x,利用勾股定理得到AB=25x,则AC=AB=25x,CH=AC﹣AH=18x,然后在Rt△BCH中,利用勾股定理计算出BC=30x,再利用正弦的定义计算sinC的值.
【解答】解:延长AI交BC于D,连结OI,作BH⊥AC于H,如图,
∵I是△ABC的内心,
∴BI平分∠ABC,即∠OBI=∠DBI,
∵OB=OI,
∴∠OBI=∠OIB,
∴∠DBI=∠OIB,
∴OI∥BD,
∵AI为⊙O的切线,
∴OI⊥AI,
∴BD⊥AD,
∵AI平分∠BAC,
∴△ABC为等腰三角形,
∴AB=AC,
在Rt△ABH中,tan∠BAH=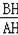
 =
=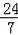
 ,
,
设BH=24x,AH=7x,
∴AB=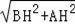
 =25x,
=25x,
∴AC=AB=25x,
∴CH=AC﹣AH=25x﹣7x=18x,
在Rt△BCH中,BC=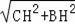
 =30x,
=30x,
∴sinC=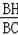
 =
=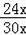
 =
=
 .
.
故选B.
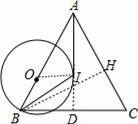

【点评】本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了等腰三角形的判定与性质.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案

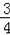
 ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.